Propriétés des limites - Définition
Voici une liste des propriétés des limites en calcul différentiel.
Propriété de la fonction constante
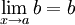
Approche graphique
Le graphique de la fonction f définie par f(x) = b est une droite d'équation y = b, la limite de la fonction est l'ordonnée à l'origine.
Propriété de la fonction f définie par f(x) = x
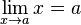
Approche graphique
Le graphique de cette fonction est une droite passant par l'origine, d'équation y = x. La limite lorsque x se rapproche de a, correspond à l'ordonnée du point d'abscisse a sur la droite, cette limite vaut donc a.
Propriété de la multiplication par une constante
Si f admet en a une limite finie et si d est une constante réelle alors la fonction

![\lim_{x \to a}[d\times f(x)] = d\times \lim_{x \to a}f(x)](https://static.techno-science.net/illustration/Definitions/autres/5/5e7a7edb374704de08cb34f374905dee_214b2cdcc8322a38b0b1b0c739acd376.png)
La limite d'une fonction multipliée par une constante est égale à la constante multipliée par la limite de la fonction.
Règle de la somme
Si les fonctions f et g admettent chacune une limite finie en a, alors la fonction f + g admet elle aussi une limite en a telle que:
![\lim_{x \to a}[f(x) + g(x)] = \lim_{x \to a} f(x) + \lim_{x \to a} g(x)](https://static.techno-science.net/illustration/Definitions/autres/8/83c9e2dc88ab860d5adaf94db4b14f37_613c4c31b50bdb6e373d4021799eaa7f.png)
La limite d'une somme est égale à la somme des limites.
Règle de la différence
Si les fonctions f et g admettent chacune une limite finie en a, alors la fonction f − g admet elle aussi une limite en a telle que:
![\lim_{x \to a}[f(x) - g(x)] = \lim_{x \to a} f(x) - \lim_{x \to a} g(x)](https://static.techno-science.net/illustration/Definitions/autres/7/7c632633cf92f37f48ec06b916cb1903_5da16ed67ff2a3afc19b96b80ec965d8.png)
La limite d'une différence est égale à la différence des limites.
Règle du produit
Si les fonctions f et g admettent chacune une limite finie en a, alors la fonction
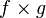
![\lim_{x \to a}[f(x) g(x)] = [\lim_{x \to a} f(x)][\lim_{x \to a} g(x)]](https://static.techno-science.net/illustration/Definitions/autres/e/e7c274868dae2facbaf02cecab6c5780_f90d6b6d15a44c43e12af7b66b2e518c.png)
La limite d'un produit est égal au produit des limites.
Règle du quotient
Si la fonction f admet une limite finie en a et si la fonction g admet une limite finie non nulle en a , alors la fonction
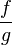
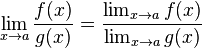
La limite d'un quotient est égal au quotient des limites (si le dénominateur n'est pas nul).
Règle des puissances
Si f admet en a une limite finie alors la fonction
![x \rightarrow [f(x)]^n](https://static.techno-science.net/illustration/Definitions/autres/5/55de74ec51d1cc3ed6c102fd5a2efcb4_a37f32b7e0591146f9049b09eccdc7ed.png)
![\lim_{x \to a}[f(x)]^n = [\lim_{x \to a}f(x)]^n](https://static.techno-science.net/illustration/Definitions/autres/3/34c3e9207b59e2b674760b1cefb07393_9def8e32c22cdeb6dc86ceec38443eb4.png)
La limite d'une fonction élevée à la puissance n est égale à la limite de la fonction, élevée à la puissance n.

















































