Intégrale (mathématiques) - Définition
Une intégrale est le résultat de l'opération mathématique, effectuée sur une fonction, appelé intégration. Une intégrale est donc composée d'un intégrande (la fonction à intégrer) et d'un opérateur que l'on appelle intégrateur (le ∫ ).
Approche intuitive
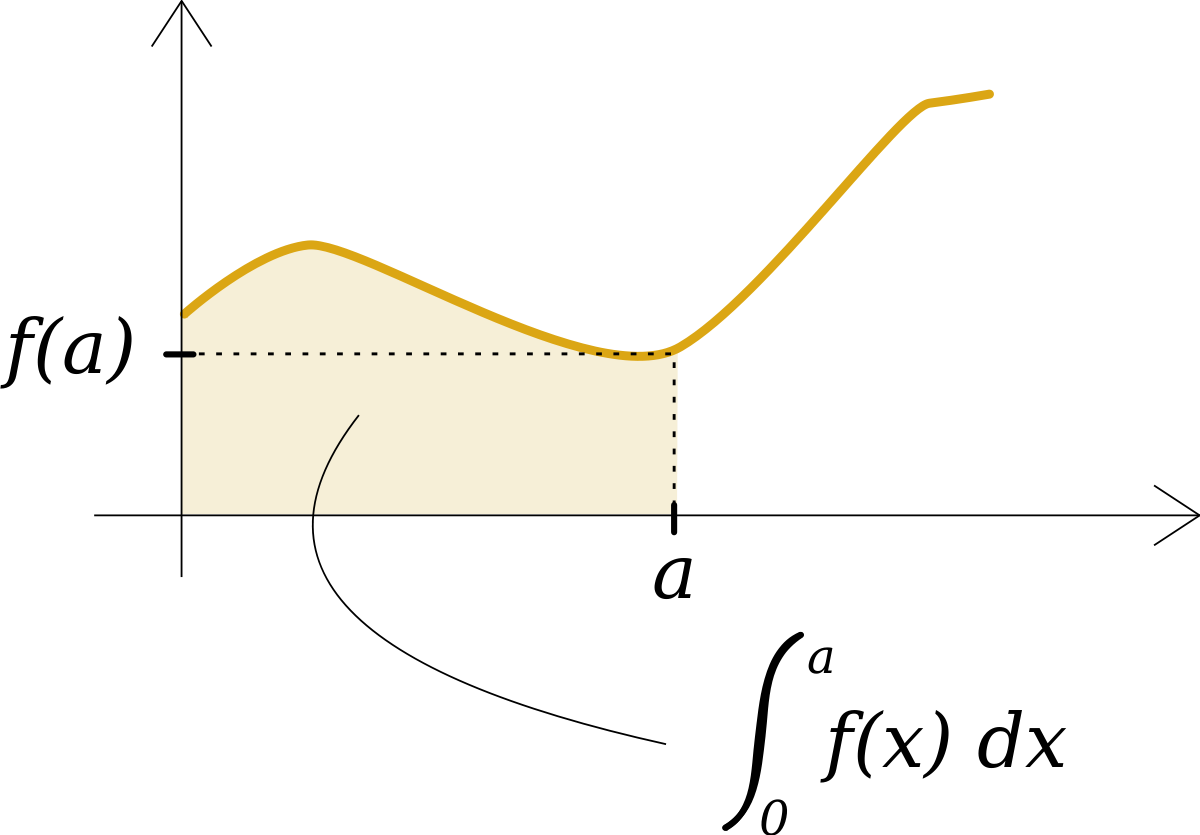
En mathématiques, l'intégrale d'une fonction réelle positive est la valeur de l'aire du domaine délimité par l'axe des abscisses et la courbe représentative de la fonction.
Pour les fonctions qui prennent des valeurs réelles négatives (gardant un signe constant par intervalles), une définition d'aire algébrique rend possible une aire négative.
Définition
Soit f une fonction continue définie sur un segment [a,b] à valeurs réelles. Pour simplifier, supposons que cette fonction soit positive (à valeurs positives ou nulles).
L'ensemble 
est une région du plan comprise entre la courbe représentative de f, les deux verticales x=a et x=b, et l'axe des abscisses x. La mesure de l'" aire " de S cherchée, notée 
, est l'intégrale de a à b de f. Celle-ci est alors appelée l'intégrale définie de f sur le segment [a,b]. Pour avoir plus de détails voir les pages intégrale de Riemann et intégrale de Lebesgue. Si une fonction est intégrable au sens de Riemann, alors elle est intégrable au sens de Lebesgue, et les deux valeurs coïncident.
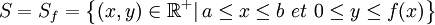
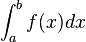
Il est possible de définir une intégrale par la notion de primitive d'une fonction. La " primitivation " est l'opération qui, à partir d'une fonction f, donne une fonction F dérivable et dont la dérivée est égale à f. F'(x) = f(x),
En admettant que toute fonction continue sur un segment [a, b], admet des primitives, l'intégrale de a à b est égale à F(b)-F(a) et ce nombre ne dépend pas de la primitive choisie.
Cette approche est motivée en analyse, et est la méthode principale utilisée pour le calcul d'aire sous une courbe comme décrit dans le paragraphe précédent.
Les fonctions qui admettent des primitives sont aussi intégrables au sens de Riemann (et aussi au sens de Lebesgue).
Le théorème fondamental du calcul différentiel et intégral affirme que les deux approches de l'intégrale (" aire sous une courbe " et " primitivation "), sont sous certaines conditions les mêmes.
La nuance entre l'intégration au sens de Riemann et au sens de Lebesgue
Le schéma général utilisé pour construire une intégrale et qui cherche à mesurer l'aire du domaine sous la courbe, est le même pour les deux approches de l'intégration, au sens de Riemann et au sens de Lebesgue.
D'abord, on considère une famille de fonctions élémentaires, pour lesquelles nous avons un moyen évident de mesurer l'aire sous la courbe. Dans le cas de l'intégrale de Riemann, ce sont les fonctions en escalier dont l'aire sous la courbe est égale à la somme des aires des rectangles ; le domaine sous la courbe d'une telle fonction peut alors être vu comme une réunion de rectangles. Pour l'intégrale de Lebesgue, les fonctions élémentaires sont appelées fonctions étagées, et les rectangles sont remplacés par des objets plus sophistiqués.
Construction
Si sur le segment [a,b], 
(ainsi Sf est inclus dans Sg), alors nous aurons 
. Si l'on suppose la fonction f monotone sur [a,b], il est possible d'approcher son aire en utilisant soigneusement une fonction élémentaire s (dans le cas de l'intégration de Riemann, une fonction en escalier, et dans le cas de l'intégration de Lebesgue, une fonction étagée). Nous choisissons s telle que 
mais en supposant s très proche de f, au sens où, ayant préalablement fixé un 
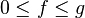
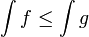
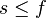
arbitrairement petit, les valeurs prises par f s'éloignent de celles prises par s d'au plus : on dit aussi ![\sup_{[a,b]}\,|f-s|\le\varepsilon](https://static.techno-science.net/illustration/Definitions/autres/a/aefec6d1a9689b0b3a8f4cad987c7f7f_0a18bf35b6f45b03ce12fdbffd07089b.png){kind=small}
ou 
.
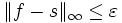
L'aire sous s, facilement calculable comme somme d'aires de rectangles, est majorée par l'intégrale de f, et est appelée somme inférieure.
Dans le cas de l'intégrale de Riemann, nous fabriquons aussi des sommes supérieures de la même façon: nous choisissons une fonction en escalier, disons σ, telle que 
en supposant σ de la même manière très proche de f, et nous considérons une somme supérieure comme un majorant de l'aire du domaine sous f. La théorie de Lebesgue n'utilise pas de sommes supérieures.
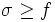
On montre que l'ensemble des aires sous les fonctions s que l'on peut choisir (respectivement sous les fonctions σ dans la théorie de Riemann), admet une borne supérieure (resp. inférieure, et c'est la même). Cette valeur est alors appelée intégrale de f sur [a,b].
Les fonctions que nous pouvons intégrer sont appelées fonctions intégrables.
Cependant, les différences commencent ici ; la théorie de Riemann est de loin la plus simple, mais de cette simplicité résulte que l'ensemble des fonctions intégrables est plus restreint que celui de la théorie de Lebesgue. En plus, l'interaction entre les limites et l'intégrale sont plus difficiles à décrire dans la théorie de Riemann.
Généralisation à un intervalle quelconque
La généralisation de l'intégrale à un intervalle quelconque se fait en se basant sur la notion d'intégrale définie sur un segment. Soit f une fonction à valeurs réelles positives, continue définie sur un intervalle I quelconque, noté (a,b), où a (resp. b) est réel ou égal à 
(resp. réel ou égal à 
), et les parenthèses signifiant [ ou ] (exclusion si valeur infinie). On dit que f est intégrable sur l'intervalle [a,b] lorsque l'ensemble 
, où S est un segment, est majoré. Partie non vide et majorée de 
, il admet une borne supérieure : on la note alors 
et on l'appelle intégrale de f sur I.
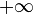
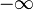
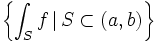
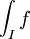
Avec ces mêmes données, on a l'équivalence logique : f intégrable sur (a,b) 
toute primitive de f sur (a,b) admet une limite finie en a et en b.
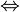
Dans le cas où une fonction f est intégrable sur un intervalle (a,b), 
.
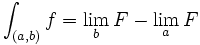
Enfin, pour une fonction continue définie sur un intervalle I quelconque et à valeurs dans 
, on pose par définition : f intégrable sur I 
intégrable sur I en tant que fonction à valeurs réelles positives.
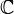
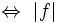
De même pour f continue définie sur I et à valeurs dans un espace vectoriel normé 
, f intégrable sur I 
intégrable sur I en tant que fonction à valeurs réelles positives.
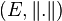
Remarque : il se peut très bien que " l'aire sous la courbe " d'une fonction définie et continue sur I et à valeurs réelles (changeant de signe) ait une limite en faisant tendre les extrémités d'une suite de segments inclus dans I vers les bornes de I, sans toutefois que la fonction en jeu soit intégrable sur I au sens de la définition. On parle alors d'intégrale semi-convergente, la valeur de l'aire trouvée est appelée Intégrale impropre. C'est le cas avec l'exemple classique de la fonction 
: elle peut être prolongée par 1 en zéro mais le problème de l'intégrabilité se pose au voisinage de . On peut calculer son intégrale impropre (puisqu'elle n'est que semi-convergente) : on trouve 
.
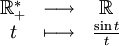
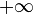
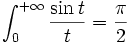
Symbole de l'intégrale
Le symbole de l'intégrale, ∫, est un ancien s long : en effet, Leibniz s'est servi de l'initiale du mot latin summa, " somme ", lequel était le plus souvent écrit ?umma. À la différence du s long, ∫, en typographie, garde toujours une hampe descendant au-dessous de la ligne de base, en romaine comme en italique.
Moyenne
- Pour toute fonction continue (ou même seulement continue par morceaux) sur un segment [a, b] non vide et non trivial (c.-à-d. b>a), la valeur moyenne de f sur [a;b] est le réel m défini par :
Cette notion généralise celle de moyenne d'un nombre fini de réels en l'appliquant à un nombre infini de valeurs prises par une fonction intégrable. Elle sert par exemple dans la décomposition en série de Fourier d'une fonction périodique : c'est la composante constante. En traitement du signal, pour les signaux périodiques, il s'agit de la composante continue (offset).
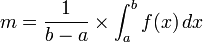
- On peut aussi, par analogie avec les moyennes pondérées d'un nombre fini de réels, affecter " à chacune des valeurs prises par la fonction " un coefficient strictement positif. On utilise alors ce que l'on appelle une fonction poids
(w pour l'initiale de weight, poids en anglais) : 
.
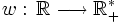
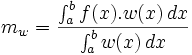
- Ce procédé peut aussi s'utiliser sur un intervalle ouvert ou semi-ouvert mais borné (ie aucune de ses bornes n'est infinie) où la fonction
est intégrable. On peut citer l'exemple classique servant à montrer l'orthogonalité de la famille des polynômes de Tchebychev : 
où la fonction 
est continue sur le fermé [0,1] et où la fonction poids est 
est intégrable sur [0,1[, et dont l'intégrale vaut 
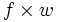
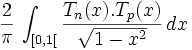
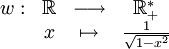
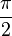
Propriétés des intégrales
Soient f et g deux fonctions continues sur I et a, b et c trois réels de I.
(relation de Chasles)
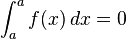
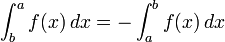
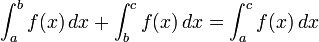
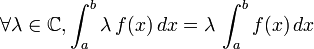
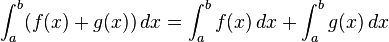
(linéarité de l'intégration - et non de l'intégrale, comme il est trop souvent dit)- Si
sur [a; b], alors 
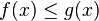
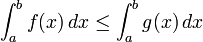
- Inégalité de la moyenne
- Si f est continue sur [a; b] et si pour tout x de cet intervalle, on a :
, alors 
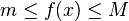
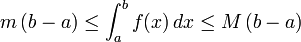
Intégration par parties
Soient u et v deux fonctions C1 (ie dérivables de dérivées continues sur [a,b]) :
![\int_{a}^{b} u'(x)v(x)\,dx = [u(x)v(x)]_a^b - \int_{a}^{b} u(x)v'(x)\,dx](https://static.techno-science.net/illustration/Definitions/autres/d/d8a2d08db8b915bca4e5536c07f85533_08f99688df9d746acca90f2b9b7e9440.png){kind=small}