Croissance exponentielle - Définition
En mathématique, en économie et en biologie, on parle d'un phénomène à croissance exponentielle (ou géométrique) lorsque la croissance en valeur absolue de la population est proportionnelle à la population existante, c'est-à-dire lorsque le taux de croissance est constant.
On exprime alors souvent la croissance sous forme d'un pourcentage : une croissance de 10 % par an signifie que la population est multipliée par 1,1 chaque année. Ainsi, pour une population initiale de 1 000 individus :
- au bout d'un an, elle passe à 1 100 individus (
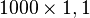
- au bout de deux ans, elle passe à 1 210 individus (
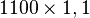
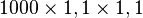
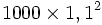
- ...
- au bout de 7 ans, elle a quasiment doublé (
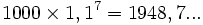
- ...
- au bout de 100 ans, elle a été multipliée par 13 780 ;
- la formule générale est
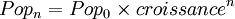
Une croissance exponentielle s'exprime en mathématiques :
- pour un phénomène discret (on prend des mesures à intervalle régulier) sous forme d'une suite géométrique
- pour un phénomène continu (on essaie de calculer ce qui se passe entre deux mesures consécutives) sous forme d'une fonction exponentielle.
On démontre en mathématiques qu'une croissance exponentielle conduit la taille de la population à croître de plus en plus vite vers

Cette évolution théorique ne résiste donc pas à l'expérience : aucun phénomène ne peut croître indéfiniment car sa croissance est limitée par le milieu dans lequel se trouve la population. Le premier à avoir soulevé un tel problème fut le pasteur Thomas Malthus (1766 - 1834), bien que ses prévisions sur la croissance de la population humaine ne se soient pas réalisées.
De nos jours, on admet volontiers que le développement bactérien d'une culture biologique peut être modélisé sous forme exponentielle pour le début du développement mais que les contraintes du milieu (nutriment, volume disponible) rendent préférable, par la suite, le choix d'un modèle de Verhulst (1838).
-
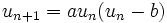
-

avec tout le caractère chaotique que peut présenter une telle fonction logistique.

















































