Analyse non standard - Définition

La naissance du calcul différentiel et infinitésimal au XVII^e siècle mena à l'introduction et à l'utilisation de quantités infiniment petites. Leibniz ou Euler en firent grand usage. Cependant, ils ne purent éclairer pleinement la nature même de ces infiniment petits. Leur usage disparut au XIX^e siècle avec le développement de la rigueur en Analyse, depuis Cauchy jusqu'à Weierstrass ou Dedekind.

Il fallut attendre la deuxième moitié du XX^e siècle pour qu'une introduction rigoureuse des infiniment petits soit proposée. En 1960, Abraham Robinson définit les infiniment petits par une ultra-puissance de , donnant ainsi naissance à une nouvelle théorie, l'analyse non standard. Peu après, Nelson fournit une présentation de l'analyse non standard plus abordable, basée sur l'axiomatique de Zermelo-Frankel à laquelle est ajouté un nouveau prédicat : le prédicat standard. Le comportement de ce nouveau prédicat est basé sur 3 axiomes nouveaux :

1. l'axiome d'idéalisation
2. l'axiome de standardisation
3. l'axiome de transfert

Ces 3 axiomes sont plus connus sous le nom IST.

Le sens du qualificatif standard donné par ces axiomes est celui d'objet appartenant à l'horizon perceptible, non standard comme étant au-delà de l'horizon perceptible. Un ensemble peut donc être standard ou non standard (on dit aussi charmé), il ne peut être les deux. Seront standard les objets usuels des mathématiques classiques (1, 2, π, ...). Les infiniments petits ou infiniments grands introduits seront non standard.

Intérêt de l'analyse non standard

Il y a deux types d'applications :

• Il a été établi qu'un énoncé classique, possédant une démonstration dans le cadre de l'analyse non standard, était vrai dans le cadre des mathématiques classiques. La situation est tout à fait comparable aux mathématiciens d'avant 1800, qui s'autorisaient à utiliser les nombres imaginaires à condition que le résultat final soit bien réel. L'analyse non standard permet donc de donner de nouvelles démonstrations (souvent plus simples) de théorèmes classiques.
• L'analyse non standard permet en outre de manipuler les concepts nouveaux de nombre infiniment petit ou d'infiniment grand qui ont posé tant de problèmes aux mathématiciens et qui avaient été bannis de l'analyse. Elle est donc plus générale que l'analyse classique, de même que l'analyse complexe est plus générale que l'analyse réelle.
• Cependant, l'analyse non standard a eu à ce jour peu d'influence. Peu de théorèmes nouveaux ont été mis au point au moyen de celle-ci, et pour le moment, elle constitue essentiellement une réécriture de l'ensemble de l'analyse au moyen de nouveaux concepts.

Les axiomes

• On se place dans le cadre de la théorie des ensembles de Zermelo-Fraenkel (celle que nous pratiquons tous sans le savoir, comme M. Jourdain).
• Les objets ou les ensembles définis par cette théorie seront qualifiés d'internes ou classiques. C'est le cas de tous les objets et ensembles usuels que nous connaissons : ...
• On introduit un nouveau prédicat, étranger à la théorie de Zermelo-Fraenkel, et qui s'applique sur les ensembles et objets internes précédents. Un tel ensemble ou objet pourra être qualifié de standard ou de non standard. Par exemple, on pourra parler d'entier standard et d'entier non standard. Le mot " standard " n'est pas défini, pas plus que ne sont définis les mots " ensemble " ou " appartenance ". Ce sont ce qu'on appelle des notions primitives. On explique seulement la façon dont on peut utiliser cette nouvelle notion, au moyen des axiomes qui suivent.

Axiome d'idéalisation

Soit R(x,y) une relation classique (une relation classique est une relation ne faisant pas intervenir le nouveau prédicat " standard " dans son énoncé. Il s'agit donc d'une relation usuelle de nos mathématiques de tous les jours). L'axiome d'idéalisation affirme que les deux propositions suivantes sont équivalentes:

1. Pour chaque partie standard finie F, il existe un élément x noté x_F tel que R(x,y) pour tous les y appartenant à F
2. Il existe un élément x de E tel que R(x,y) pour tout y standard

L'axiome signifie que, pour trouver un élément x qui vérifie une propriété relative à tous les éléments y standard, il faut et il suffit de trouver un tel x relatif aux éléments y de n'importe quel ensemble standard fini.

Exemple 1 : Il existe un entier supérieur à tous les entiers standard

Nous voulons montrer que : il existe x entier, tel que, pour tout y standard entier, x > y. Soit donc R(x,y) défini par : x est entier et y est entier et x > y. La proposition 1 de l'axiome d'idéalisation est bien vérifié : si F est fini (standard ou non d'ailleurs), il existe bien un entier x supérieur aux entiers y éléments de F. Par conséquent, l'axiome d'idéalisation énonce que la proposition 2 est aussi vérifiée et celle-ci correspond à notre énoncé.

Il existe donc un entier x supérieur à tous les nombres entiers standard. Cet entier sera donc non standard, sinon, il serait supérieur à lui-même. Nous venons donc de montrer qu'il existe au moins un entier non standard. Les entiers supérieurs à x sont a fortiori non standard, sinon, x leur serait supérieur. Pour cette raison, dans l'ensemble des entiers, les entiers non standard sont également qualifiés d'inaccessibles, ou d'illimités, ou d'infiniment grands. Le terme " illimité " est peut-être mal choisi. Il pourrait faire croire que de tels entiers sont infinis. Mais tous les entiers sont finis ! Nous préférons donc le terme d'inaccessible ou d'infiniment grand. Les entiers non standard sont aussi appelés hypernaturels.

Exemple 2 : Tout ensemble infini possède un élément non standard

Considérons la relation x différent de y dans un ensemble E infini. Pour chaque partie finie standard F, nous trouvons un élément x noté x_F appartenant à E tel que x soit différent de y pour tout y appartenant à F, puisque E est infini.

L'axiome d'idéalisation fournit alors l'existence d'un élément charmé (ou non standard) x appartenant à E et différent de tous les éléments standard y appartenant à E.

On en déduit la propriété suivante :

Dans tout ensemble infini, il y a au moins un élément charmé.

et par contraposition :

Si tous les éléments d'un ensemble sont standard, cet ensemble E est fini.(1)

Exemple 3 : Théorème de Nelson

Ce théorème énonce que, si E est un ensemble, il existe une partie finie X de E contenant tous les éléments standard de E. Les éléments standard d'un ensemble sont donc en nombre fini. On définit pour cela la relation R(X,y) suivante : X est inclus dans E, X est fini et si y est élément de E, alors y est élément de X. La proposition 1 de l'axiome d'idéalisation est bien vérifée pour toute partie finie F (standard ou non d'ailleurs) en prenant X l'intersection de F et E. Par conséquent, la proposition 2 de l'axiome d'idéalisation permet de valider le théorème de Nelson.

On notera que la partie X donnée par l'axiome est une partie interne ou classique. Elle ne se limite pas nécessairement aux seuls éléments standard de E, car, a priori, la collection des éléments standard, définie à partir de la relation non classique " être standard " est un objet externe, c'est-à-dire étranger aux mathématiques usuelles. En effet, la relation "être standard" ne fait pas partie des relations auxquelles s'appliquent les axiomes de ZFC, ce qui veut dire qu'il n'existe pas d'ensemble ne contenant que les entiers standards. Ainsi, dans les entiers, un ensemble X contenant tous les entiers standard est de la forme {0, 1, 2, ..., n} avec n non standard, et cet ensemble contient aussi des entiers non standard.

Axiome de transfert

Dès que tous les paramètres E_i d'une valeur classique F ont des valeurs standard :

Pour tout x standard , F(x,E₁, ...,E_n) si et seulement si pour tout x, F(x,E₁, ...,E_n)

Autrement dit, pour vérifier qu'une formule usuelle dépendant de paramètres standard est vraie pour tout x, il suffit de la vérifier pour tout x standard. Intuitivement, nous ne pouvons accéder qu'aux éléments standard, et ce sont eux qui nous permettront de vérifier une formule classique. Cet axiome peut aussi s'exprimer (par négation) :

Il existe x standard, F(x,E₁, ...,E_n) si et seulement s’il existe x, F(x,E₁, ...,E_n)

Si une propriété classique est vraie pour un x, alors elle est vraie pour un x standard. En voici quelques conséquences. La plus importante est le fait que si un objet mathématique est défini de façon classique de manière unique à partir d'objets standard, il est nécessairement standard. C'est donc le cas de pour n standard. De même, si E et F sont des ensembles standard, il en est de même de leur intersection, de leur réunion, de leur produit, de l'ensemble des applications de E dans F, de l'ensemble des parties de E. Si a et b sont deux nombres standard, il en est de même de ab, a+b, a–b, a/b, etc. Si n est standard, il en est de même de n+1 ou de I_n = {1, ..., n}. Si A est une partie standard de bornée, Sup A et Inf A sont standard. Si f est une fonction standard (c’est-à-dire définie sur des ensembles standard et de graphe standard), alors l'image d'un élément standard est standard.

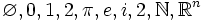
Enfin, cet axiome permet de montrer que, pour voir que deux ensembles standard sont égaux, il suffit de vérifier qu'ils possèdent les mêmes éléments standard. Ainsi, la seule partie standard de contenant tous les entiers standard est lui-même. Par contre, il existe des parties non standard contenant tous les entiers standard, à savoir les parties {0, 1, 2, ..., n} avec n non standard.

Axiome de standardisation

Soit E un ensemble standard, soit P une propriété quelconque, faisant ou non intervenir le postulat " standard ". Alors :

Il existe un ensemble A standard tel que pour tout x standard, x appartient à A si et seulement si x appartient à E et vérifie P(x)

Cet axiome ne présente d'intérêt que si la propriété P est non classique (elle utilise le postulat " standard "). A n'est autre qu'un ensemble standard dont les éléments standard sont les éléments standard de E vérifiant la propriété P. Il se peut que A possède d'autres éléments, mais ils seront non standard. Par ailleurs, un ensemble standard étant défini de maniére unique par ces éléments standard, il en résulte que A est unique. On l'appelle le standardisé de la collection {x élément de E | P(x)} qui, a priori, n'est pas un ensemble au sens ZFC. L'interprétation intuitive qu'on peut donner à cet axiome est le suivant : la collection {x élément de E | P(x)} ne nous est pas directement accessible. Nous ne pouvons concevoir que son standardisé. Nous insistons sur le fait que, si la propriété P utilise le postulat " standard ", cette propriété est étrangère à l'axiomatique de Zermelo-Fraenkel (puisque le mot " standard " ne fait pas partie de cette axiomatique), et donc que la collection {x élément de E | P(x)} n'est pas un ensemble au sens de Zermelo-Fraenkel, c'est pourquoi nous la qualifions de collection. (plus techniquement, la propriété P n'est pas nécessairement collectivisante, et la notation {x élément de E | P(x)} est formellement aussi illégale que le serait, par exemple, {x | x=x} pour désigner l'ensemble de tous les ensembles).

Par exemple, considérons E = , et P(x) la propriété x est standard. La collection {x élément de E | P(x)} est la collection des éléments standard. Son standardisé est un ensemble standard contenant tous les éléments standard de . Nous avons déjà vu qu'il s'agissait de lui-même.

Considérons maintenant E = , et P(x) la propriété x est non standard. La collection {x élément de E | P(x)} est la collection des éléments non standard. Son standardisé est l'ensemble vide.

Les nombres en analyse non standard

Les entiers

Rappelons que nous qualifions d'internes ou classiques les propriétés ou les ensembles n'utilisant pas le mot " standard ". Nous appelons externes ou non classiques les propriétés utilisant ce mot. Toutes les propriétés connues classiques restent valides en Analyse non standard. Ainsi, vérifie l'axiome de récurrence, pourvu que cet axiome soit appliqué à une propriété classique.

En revanche, le prédicat standard étant non classique, l'axiome de récurrence ne s'y applique pas. Ainsi, 0 est standard ; si n est standard, n + 1 aussi. Cependant, il existe des entiers non standard supérieurs à tous les entiers standard. De tels entiers non standard sont appelés infiniment grand.

Tout entier standard est inférieur à tout entier non standard. Si n est non standard, il en de même des éléments supérieurs à n et de n – 1. On peut voir comme suit :

0 1 2 3 . . . . . . . . . n-1 n n+1 . . .

entiers standard suivis des entiers non standard

On ne peut parler du plus petit entier non standard, pas plus que nous ne pouvons parler du plus grand entier standard, car ces ensembles ne sont pas classiques, et on ne peut donc pas leur appliquer les propriétés classiques de .

Si P est une propriété quelconque, on montre que vérifie le principe de récurrence restreint suivant :

si P(0) est vrai, et si pour tout n standard, P(n) implique P(n+1), alors pour tout n standard, P(n) est vérifié.

Les réels

On montre qu'on peut partitionner l'ensemble des réels en :

• les infinitésimaux ou infiniment petits, inférieurs en valeur absolue à tout réel standard. À part 0, ils sont non standard. x – y infinitésimal est noté x ≈ y. On dit que x et y sont infiniment proches.
• les illimités, supérieur en valeur absolue à tout réel (ou tout entier) standard. Ils sont non standard. Leurs inverses sont infinitésimaux.
• les appréciables. Les appréciables et les infinitésimaux font partie des réels limités.

Par exemple : 0,000...01 est infiniment petit si le nombre de 0 est un entier infiniment grand. Ce nombre est alors infiniment proche de 0.

Si n est un entier infiniment grand, alors 1/n est infiniment petit.

On montre également que, pour chaque réel limité x, il existe un unique réel °x standard tel que la différence x – °x soit infinitésimale. °x s'appelle partie standard de x.

Par exemple, 0,3333.....333 où le nombre de 3 est un entier infiniment grand est un réel limité non standard, dont la partie standard est 1/3.

Tout réel limité se décompose de manière unique sous la forme standard + infinitésimal.

Les réels infiniment proches d'un réel donné constituent le halo de ce réel.

Les suites en analyse non standard

Nous allons donner des propriétés non classiques des suites, qui, dans le cas des suites standard, coïncideront avec des propriétés usuelles.

Convergence d'une suite

Pour une suite standard (a_n), il y a équivalence entre :

1. la suite (a_n) converge vers l
2. l est standard et, pour tout n infiniment grand, a_n ≈ l

En effet, si (a_n) est standard et converge vers l, sa limite est standard (par transfert) et vérifie :

pour tout ε > 0, il existe N tel que, pour tout n > N, | a_n - l | < ε

Par transfert, on a alors :

pour tout ε standard > 0, il existe N standard tel que, pour tout n > N, | a_n - l |

Si on prend n infiniment grand, n est alors supérieur à N donc | a_n - l | < ε, et cette inégalité étant vérifiée pour tout ε standard, on a bien a_n ≈ l

Réciproquement, si, pour tout n infiniment grand, a_n ≈ l avec l standard, alors :

pour tout ε standard > 0, il existe N tel que, pour tout n > N, | a_n - l | < ε

Il suffit en effet de prendre N infiniment grand.

et par transfert :

pour tout ε > 0, il existe N tel que, pour tout n > N, | a_n - l | < ε

ce qui est la définition de la convergence.

On notera bien que l'équivalence énoncée n'est valide que pour les suites standard. Si on définit en effet a_n = ( − 1)ⁿα avec α infiniment petit, alors a_n ≈ 0 pour tout n et pourtant la suite (a_n) ne converge pas (mais cette suite n'est pas une suite standard).

Convergence d'une sous-suite

Pour une suite (a_n) standard, il y a équivalence entre :

1. il existe une sous-suite de (a_n) qui converge vers l
2. l est standard et il existe n illimité tel que (a_n) ≈ l

En effet, si l est limite d'une sous-suite de (a_n), alors l est standard par transfert, et pour tout ε > 0, il existe une infinité de n tel que | a_n - l | < ε. Cette propriété est donc vraie pour ε infiniment petit, et comme elle est vérifiée par une infinité de n et qu'il n'existe qu'un nombre fini d'entiers standard, il existe donc n infiniment grand tel que | a_n - l | < ε. Mais comme ε est infiniment petit, cela signifie que (a_n) ≈ l.

Réciproquement, s'il existe n illimité tel que (a_n) ≈ l, alors :

pour tout ε standard > 0, pour tout N standard, il existe n > N, | a_n – l | < ε

er par transfert :

pour tout ε > 0, pour tout N , il existe n > N, | a_n – l | < ε

ce qui exprime que l est valeur d'adhérence de la suite (a_n) et dans ce cas, il existe bien une sous-suite de (a_n) qui converge.

On en déduit le théorème de Bolzano-Weierstrass, qui exprime, que, de toute suite réelle bornée, on peut extraire une sous-suite qui converge. Par transfert, il suffit de montrer ce théorème sur les suites standard. Soit donc (a_n) une suite standard bornée. Tous ses termes sont limités car, par transfert, on peut prendre un majorant et un minorant de (a_n) standard. On prend alors n illimité et l = °a_n partie standard de a_n. On applique alors l'équivalence montrée précédemment, la propriété 2 étant vérifiée.

Suite de Cauchy

Pour une suite (a_n) standard, il y a équivalence entre :

1. (a_n) est une suite de Cauchy
2. pour tout n et p illimités, a_n ≈ a_p

La démonstration suit une démarche comparable à celles des paragraphes précédents.

Montrons que, dans , toute suite de Cauchy converge. Par transfert, il suffit de montrer cette propriété sur les suites standard. Soit (a_n) une telle suite. Elle est bornée : en effet, il n'y a qu'un nombre fini d'entiers standard, et tous les a_n avec n illimités sont dans le même halo de l'un d'entre eux. Par transfert, la borne peut être choisie standard. Tous les termes de la suite sont donc limités. On prend alors l = °a_p partie standard de a_p avec p illimité. Alors, pour tout n illimité, a_n ≈ a_p ≈ l, donc la suite converge vers l.

Les fonctions en analyse non standard

Continuité

La continuité d'une fonction dans se définit plus simplement avec l'analyse non standard. Pour une fonction standard, il y a équivalence entre

1. f est continue
2. pour tout y infiniment petit et pour tout x standard, f(x + y) est infiniment proche de f(x).

On montre le théorème des valeurs intermédiaires de la façon suivante. Soit f continue sur un segment [a,b] avec f(a) < 0 et f(b) > 0. Alors il existe c entre a et b tel que f(c) = 0. En effet, par transfert, il suffit de montrer ce théorème pour f, a et b standard. Soit N un entier illimité et pour k entre 0 et N. Si K est le premier k pour lequel alors on prendra pour c la partie standard de x_K. On a effet c infiniment proche de x_K et de x_{K − 1}, de sorte que f(c) sera infiniment proche du réel positif ou nul f(x_K) et infiniment proche du réel négatif f(x_{K − 1}). Etant standard, f(c) est nul.

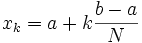
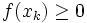
On montre d'une façon comparable que f admet un maximum et un minimum.

Continuité uniforme

Pour une fonction standard, il y a équivalence entre

1. f est uniformément continue
2. pour tout y infiniment petit et pour tout x, f(x + y) est infiniment proche de f(x).

Par exemple, la fonction qui à x associe x² est continue, puisque, si x est standard et y infiniment petit, on a :

(x+y)² = x² + 2xy + y² ≈ x² puisque x étant limité, xy est infiniment petit, ainsi que y²

Par contre, cette fonction n'est pas uniformément continue puisque, si x est infiniment grand et si y = 1/x, alors (x+y)² = x² + 2 + y² qui n'est pas infiniment proche de x².

Sur un segment [a,b], toute fonction continue f est uniformément continue. Par transfert, il suffit de montrer cette propriété pour f, a et b standard. Les éléments du segment sont alors tous limités, donc admettent tous une partie standard. Si x est élément de [a,b], °x sa partie standard et y infiniment petit, on a :

f(x+y) = f(°x + z) avec z = y + x - °x infiniment petit

donc f(x+y) ≈ f(°x) ≈ f(x) par continuité de f en °x

Dérivation

Pour une fonction standard définie sur un intervalle standard de , et pour x₀ standard il y a équivalence entre :

1. f est dérivable en x₀ de dérivée l
2. pour tout x infiniment proche de x₀, ≈ l, avec l standard.

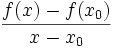
Intégration

Pour une fonction standard f sur [a , b] = I standard , il y a équivalence entre

1. f intégrable au sens de Riemann
2. pour toute subdivision de [a,b] a = x₀ < x₁ < ... < x_n = b avec x_i ≈ x_i+1, il existe deux fonctions en escalier φ et ψ relatives à la subdivision de façon que, pour tout x de I, φ(x) ≤ f(x) ≤ ψ(x), et ≈ 0. On pose alors la partie standard de ou de .

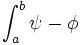
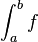
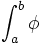
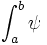
Notions diverses

Nous donnons ci-dessous des exemples d'équivalent en analyse non standard de notions de l'analyse classique, lorsqu'elles sont appliquées à des objets standard. Celles-ci ont pour but de montrer l'ampleur des domaines à explorer.

• Convergence simple vers f d'une suite (f_n) de fonctions : pour tout n infiniment grand et tout x standard, f_n(x) ≈ f(x).
• Convergence uniforme vers f d'une suite (f_n) de fonctions : pour tout n infiniment grand et tout x, f_n(x) ≈ f(x).
• Compacité d'un espace K : tout point de K est presque stantard (un point est presque standard s'il est infiniment proche d'un point standard)
• Complétude d'un espace E : tout point quasi standard est presque standard (un point x est quasi standard si pour tout r standard, x se trouve à une distance inférieure à r d'un point standard)

Bibliographie

• Alain Robert, Analyse non standard, Presses polytechniques romandes, 1985
• E.Nelson, Internal set Theory, a new approach to NSA, Bull.AMS, 83 (1977) pp 1165-1198
• E.Nelson, Radically Elementary Probability Theory, Princeton University Press, 1987
• E.Nelson, Théorie radicalement élémentaire des probabilités (traduction), http://www.math.princeton.edu/~nelson/books/rept/rept.pdf
• Gödel, Escher, Bach – Douglas Hofstader (InterEditions 1985)
• Leçons de calcul infinitésimal – André Deledicq/Marc Diener (Armand Colin 1989)
• Analyse non standard – F. Diener, G. Reeb (Hermann 1989)