Statistiques - Définition

La statistique (par opposition à une statistique) est l'ensemble des instruments et de recherches mathématiques permettant de déterminer les caractéristiques d'un ensemble de données (généralement vaste). Les statistiques (au pluriel) sont le produit des analyses reposant sur l'usage de la statistique. Cette activité regroupe trois principales branches :

• la collecte des données ;
• le traitement des données collectées, aussi appelé la statistique descriptive ;
• l'interprétation des données, aussi appelée l'inférence statistique, qui s'appuie sur la théorie des sondages et la statistique mathématique.

Cette distinction ne consiste pas à définir plusieurs domaines étanches. En effet, le traitement et l'interprétation des données ne peuvent se faire que lorsque celles-ci ont été récoltées. Réciproquement, la statistique mathématique précise les règles et les méthodes sur la collecte des données, pour que celles-ci puissent être correctement interprétées.

John Tukey disait qu'il y a deux approches en statistiques, entre lesquelles on jongle constamment : les statistiques exploratoires et les statistiques confirmatoires (exploratory and confirmatory statistics) :

• on explore d'abord les données pour avoir une idée qualitative de leurs propriétés ;
• puis on fait des hypothèses de comportement que l'on confirme ou infirme en recourant à d'autres techniques statistiques.

Histoire

Bien que le nom de statistique soit relativement récent — on attribue en général l'origine du nom au XVIII^e siècle de l'allemand Staatskunde — cette activité semble exister dès la naissance des premières structures sociales. D'ailleurs, les premiers textes écrits retrouvés étaient des recensements du bétail, des informations sur son cours, et des contrats divers. On a ainsi trace de recensements en Chine au XXIII^e siècle av. J.-C. ou en Égypte au XVIII^e siècle av. J.-C.. Ce système de recueil de données se poursuit jusqu'au XVII^e siècle. En Europe, le rôle de collecteur est souvent tenu par des guildes marchandes puis par les intendants de l'État.

Ce n'est qu'au XVIII^e siècle que l'on vit apparaître le rôle prévisionnel des statistiques avec la construction des premières tables de mortalité.

La statistique mathématique s'appuya sur les premiers travaux concernant les probabilités développés par Fermat et Pascal. C'est probablement chez Thomas Bayes que l'on vit apparaître un embryon de statistique inférentielle. Condorcet et Laplace parlaient encore de probabilité là où l'on parlerait aujourd'hui de fréquence. Mais c'est à Adolphe Quételet que l'on doit l'idée que la statistique est une science s'appuyant sur les probabilités.

Le XIX^e siècle vit cette activité prendre son plein essor. Des règles précises sur la collecte et l'interprétation des données sont édictées. La première application industrielle des statistiques eut lieu avec le recensement américain de 1890, qui mit en œuvre la carte perforée inventée par le statisticien Herman Hollerith. Celui-ci avait déposé un brevet au bureau américain des brevets.

Au XX^e siècle, ces applications industrielles se développèrent d'abord aux États-Unis, qui étaient en avance sur les sciences de gestion, puis seulement après la Première Guerre mondiale en Europe. Le régime nazi employa des méthodes statistiques à partir de 1934 pour le réarmement. En France, on était moins au fait de ces applications.

L'application industrielle des statistiques en France se développa avec la création de l'INSEE, qui remplaça le Service National des Statistiques créé par René Carmille.

L'avènement de l'informatique dans les années 1940 (aux États-Unis) puis en Europe (dans les années 1960) permit de traiter un plus grand nombre de données, mais surtout de croiser entre elles des séries de données de types différents. C'est le développement de ce qu'on appelle l'analyse multidimensionnelle. Au cours de ce même siècle, plusieurs courants de pensée vont s'affronter :

• les objectivistes ou fréquentistes qui pensent que les probabilités fournissent un modèle permettant d'idéaliser la distribution en fréquence et que là s'arrêtent leur rôle.
• les subjectivistes qui voient les probablités comme un moyen de mesurer la confiance que l'on peut avoir dans une prévision.
• les néo-bayesiens qui soutiennent que les données statistiques seules ne permettent pas de donner le modèle probabiliste idéalisant la distribution en fréquence: il est nécessaire de proposer au départ une forme général du modèle.

Domaines d'application

Les statistiques sont utilisées dans des domaines très variés comme :

• En géophysique, pour les prévisions météorologiques, la climatologie, la pollution, les études des rivières et des océans,
• En démographie : Le recensement permet de faire une photographie à un instant donné d'une population et permettra par la suite des sondages dans des échantillons représentatifs,
• En sciences économiques et sociales, et en économétrie : l'étude du comportement d'un groupe de population ou d'un secteur économique s'appuie sur des statistiques. C'est dans cette direction que travaille l'INSEE. Les questions environnementales s'appuient également sur des données statistiques.
• En sociologie : les sources statistiques constituent des matériaux d'enquête, et les méthodes statistiques sont utilisées comme techniques de traitement des données ; le sondage d'opinion devient un outil pour la décision ou l'investissement,
• En physique : l'étude de la mécanique statistique et de la thermodynamique statistique (cf Physique statistique) permet de déduire du comportement de particules individuelles un comportement global (passage du microscopique au macroscopique),
• En métrologie, pour tout ce qui concerne les systèmes de mesure et les mesures elles-même,
• En médecine, tant pour le comportement des maladies que leur fréquence ou la validité d'un traitement ou d'un dépistage.

Statistique descriptive et statistique mathématique

Le but de la statistique est d'extraire des informations pertinentes d'une liste de nombres difficile à interpréter par une simple lecture. Deux grandes familles de méthodes sont utilisées selon les circonstances. Rien n'interdit de les utiliser en parallèle dans un problème concret mais il ne faut pas oublier qu'elles résolvent des problèmes de natures totalement distinctes. Selon une terminologie classique, ce sont la statistique descriptive et la statistique mathématique. Aujourd'hui, il semble que des expressions comme analyse des données et statistique inférentielle soient préférées, ce qui est justifié par le progrès des méthodes utilisées dans le premier cas.

Considérons par exemple les notes globales à un examen. Il peut être intéressant d'en tirer une valeur centrale qui donne une idée synthétique sur le niveau des étudiants. Celle-ci peut être complétée par une valeur de dispersion qui mesure, d'une certaine manière, l'homogénéité du groupe. Si on veut une information plus précise sur ce dernier point, on pourra construire un histogramme ou, d'un point de vue légèrement différent, considérer les déciles. Ces notions peuvent être intéressantes pour faire des comparaisons avec les examens analogues passés les années précédentes ou en d'autres lieux. Ce sont les problèmes les plus élémentaires de l'analyse des données qui concernent une population finie. Les problèmes portant sur des statistiques multidimensionnelles nécessitent l'utilisation de l'algèbre linéaire. Indépendamment du caractère, élémentaire ou non, du problème il s'agit de réductions statistiques de données connues dans lesquelles l'introduction des probabilités améliorerait difficilement l'information obtenue. Il est raisonnable de regrouper ces différentes notions :

• Statistique descriptive pour les notions élémentaires,
• Analyse en composantes principales,
• Analyse factorielle des correspondances;
• Analyse Discriminante,
• Visualisation des données,
• etc.

Un changement radical se produit lorsque les données ne sont plus considérées comme une information complète à décrypter selon les règles de l'algèbre mais comme une information partielle sur une population plus importante, généralement considérée comme une population infinie. Pour induire des informations sur la population inconnue il faut introduire la notion de loi de probabilité. Les données connues constituent dans ce cas une réalisation d'un échantillon, ensemble de variables aléatoires supposées indépendantes (voir Loi de probabilité à plusieurs variables). La théorie des probabilités permet alors, entre autres opérations,

• d'associer les propriétés de l'échantillon à celles qui sont prêtées à la loi de probabilité, inconnue en toute rigueur, c'est l'échantillonnage,
• de déduire inversement les paramètres de la loi de probabilité des informations que donne l'échantillon, c'est l'estimation,
• de déterminer un intervalle de confiance qui mesure la validité de l'estimation,
• de procéder à des tests d'hypothèse, le plus utilisé étant le Test du χ² pour mesurer l'adéquation de la loi de probabilité choisie à l'échantillon utilisé,
• etc.

Statisticien

Le métier

Le statisticien utilise des statistiques théoriques et appliquées dans le secteur privé et le secteur public. Le cœur du travail est de mesurer, interpréter et décrire le monde en combinant généralement l'interprétation statistique avec des fortes connaissances sur le domaine d'étude.

Les domaines d'applications sont très variés: la production, la recherche, les finances, la médecine, l'assurance et les statistiques descriptives au sujet de la société. Les statisticiens sont souvent employés en tant qu'aide à la décision. Ils effectuent des recherches sur des concepts, des théories, des procédés et des méthodes statistiques, sous leurs aspects mathématiques et autres, les améliorent, et donnent des avis sur leurs applications dans des domaines tels que le commerce, la médecine, les sciences sociales et autres, ou les appliquent eux-mêmes.

Leurs tâches consistent:

1. à étudier, améliorer et mettre au point des théories et des méthodologies statistiques;
2. à préparer et organiser des enquêtes et d'autres collectes de données statistiques, et à mettre au point des questionnaires;
3. à évaluer, traiter, analyser et interpréter des données statistiques et à les préparer en vue de leur publication;
4. à donner des avis sur divers modes de collecte des données, sur des méthodes et techniques statistiques, ou à les appliquer eux mêmes, et à déterminer la fiabilité des résultats de leur application, en particulier dans des domaines tels que le commerce ou la médecine ainsi que d'autres secteurs des sciences naturelles, des sciences sociales ou des sciences de la vie;
5. à préparer des communications scientifiques et des rapports;
6. à s'acquitter de fonctions connexes;
7. à surveiller d'autres travailleurs.

Parmi les professions qui entrent dans ce groupe de base figurent les suivantes: Démographe, Statisticien, Statisticien mathématicien,Statisticien en statistiques appliquées

Parmi les professions apparentées, classées ailleurs, figurent les suivantes: Assistant statisticien, Employé, service statistique

Statisticiens célèbres

Voir article détaillé : Liste de statisticiens

• J.P. Benzecri - l'inventeur de l'analyse des données^{citation nécessaire}
• John Tukey - l'inventeur de l'analyse exploratoire des données
• C. Hayashi - l'inventeur de la science des données^{citation nécessaire}

La démarche statistique

Recueil des données

L'enquête statistique est toujours précédée d'une phase où sont déterminés les différents caractères à étudier.

L'étape suivante consiste à choisir la population à étudier. Il se pose alors le problème de l'échantillonnage : choix de la population à sonder (au sens large : cela peut être un sondage d'opinion en interrogeant des humains, ou bien le ramassage de roches pour déterminer la nature d'un sol en géologie), la taille de la population et sa représentativité.

• Voir article détaillé : Plan d'expérience

Que ce soit pour un recueil total (recensement) ou partiel (sondage), des protocoles sont à mettre en place pour éviter les erreurs de mesures qu'elles soitent accidentelles ou répétitives (biais).

• Voir articles détaillés : Erreur (métrologie), Erreur statistique.

Le pré traitement des données est extrêmement important, en effet, une transformation des données initiales (un passage au log, par exemple), peuvent considérablement faciliter les traitements statistiques suivants.

Traitement des données

• Voir article détaillé : statistique descriptive

Le résultat de l'enquête statistique est une série de chiffres (tailles, salaires) ou de données qualitatives (langues parlées, marques préférées). Pour pouvoir les exploiter, il va être nécessaire d'en faire un classement et un résumé visuel ou numérique. Il sera parfois nécessaire d'opérer une compression de données. C'est le travail de la statistique descriptive. Il sera différent selon que l'étude porte sur une seule variable ou sur plusieurs variables.

Étude d'une seule variable

Le regroupement des données, le calcul des effectifs, la construction de graphiques permet un premier résumé visuel du caractère statistique étudié. Dans le cas d'un caractère quantitatif continu, l'histogramme en est la représentation graphique la plus courante.

• Voir article détaillé : Représentations graphiques de données statistiques

Les valeurs numériques d'un caractère statistique se répartissent dans , il est nécessaire de définir leurs positions. En statistiques, on est en général en présence d'un grand nombre de valeurs. Or, si l'intégralité de ces valeurs forme l'information, il n'est pas aisé de manipuler plusieurs centaines voire milliers de chiffres, ni d'en tirer des conclusions. Il faut donc calculer quelques valeurs qui vont permettre d'analyser les données : c'est le rôle des réductions statistiques. Celles-ci peuvent être extrêmement concises, réduites à un nombre : c'est le cas des valeurs centrales et des valeurs de dispersion. Certaines d'entre elles (comme la variance) sont élaborées pour permettre une exploitation plus théorique des données (voir Inférence statistique)

• Voir articles détaillés : critères de position, critères de dispersion.

On peut aussi chercher à comparer deux populations. On s'interessera alors plus particulièrement à leurs critères de position, de dispersion, à leur boîte à moustaches ou à l'analyse de la variance.

Étude de plusieurs variables

Les moyens informatiques permettent aujourd'hui d'étudier plusieurs variables simultanément. Le cas de deux variables va donner lieu à la création d'un nuage de points, d'une étude de corrélation (mathématiques) éventuelle entre les deux phénomènes ou étude d'une régression linéaire .

Mais on peut rencontrer des études sur plus de deux variables : c'est l'analyse multidimensionnelle dans laquelle on va trouver l'analyse en composantes principales, l'analyse en composantes indépendantes, la régression linéaire multiple et le data mining. Aujourd'hui, le data mining (appelé aussi Knowledge Discovery) s'appuie sur la statistique pour découvrir des relations entre les variables de très vastes bases de données. Les avancées technologiques (augmentation de la fréquence des capteurs disponibles, des moyens de stockage, et de la puissance de calcul) donnent au data mining un vrai intérêt.

Interprétation et analyse des données

L'inférence statistique a pour but de faire émerger des propriétés d'un ensemble de variables connues uniquement à travers quelques une de ses réalisations (qui constituent un échantillon de données).

Elle s'appuie sur les résultats de la statistique mathématique, qui applique des calculs mathématiques rigoureux concernant la théorie des probabilités et la théorie de l'information aux situations où on n'observe que quelques réalisations (expérimentations) du phénomène à étudier.

Sans la statistique mathématique, un calcul sur des données (par exemple une moyenne), n'est qu'un indicateur. C'est la statistique mathématique qui lui donne le statut d'estimateur dont on maîtrise le biais, l'incertitude et autres caractéristiques statistiques. On cherche en général à ce que l'estimateur soit sans biais, convergeant et efficace.

On peut aussi émettre des hypothèses sur la loi générant le phénomène général, par exemple "la taille des enfants de 10 ans en France suit-elle une loi gaussienne ?". L'étude de l'échantillon va alors valider ou non cette hypothèse : c'est ce qu'on appelle les tests d'hypothèses. Les tests d'hypothèses permettent de quantifier la probabilité avec laquelle des variables (connues seulement à partir d'un échantillon) vérifient une propriété donnée.

Enfin, on peut chercher à modéliser un phénomène a posteriori. La modélisation statistique doit être différenciée de la modélisation physique. Dans le second cas des physiciens (c'est aussi vrai pour des chimistes, biologistes, ou tout autre scientifique), cherchent à construire un modèle explicatif d'un phénomène, qui est soutenu par une théorie plus générale décrivant comment les phénomènes ont lieu en exploitant le principe de causalité. Dans le cas de la modélisation statistique, le modèle va être construit à partir des données disponibles, sans aucun a priori sur les mécanismes entrant en jeux. Ce type de modélisation s'appelle ausssi modélisation empirique. Bien entendu, compléter une modélisation statistique par des équations physiques (souvent intégrées dans les pré traitements des données) est toujours positif.

Un modèle est avant tout un moyen de relier des variables à expliquer Y à des variables explicatives X, par une relation fonctionnelle :

Y = F(X)

Les modéles statistiques peuvent être regroupés en grandes familles (suivant la forme de la fonction F):

• les modèles linéaires
• les modèles non linéaires
• les modèles non paramétriques

Les modèles bayésiens (du nom de Bayes) peuvent être utilisés dans les trois catégories.

Statistique mathématique

• Voir article détaillé : statistique mathématique

Cette branche des mathématiques, très liée aux probabilités, est indispensable pour valider les hypothèses ou les modèles élaborés dans la statistique inférentielle. La théorie mathématiques des probabilités formalise les phénomènes aléatoires. Les statistiques mathématiques se consacrent à l'étude de phénomènes aléatoires que l'on connaît via certaines de ses réalisations.

Par exemple, pour une partie de dés à six faces :

• Le point de vue probabiliste est de formaliser un tel jeu par une distribution de probabilité associée aux événements la première, deuxième, ..., sixième face est tirée. La théorie des probabilités nous dit par exemple que pour que cette distribution soit une distribution de probabilité, il est nécessaire que . On peut alors étudier différentes propriétés de ce jeu.
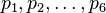
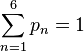
• Une fois cela fixé, les statistiques s'intéressent alors à ce genre de question: "si au bout de 100 parties, chaque face n a été tirée f_n fois, puis-je avoir une idée de la valeur des probabilités "? Avec quelle degré de confiance ?

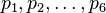
Une fois la règle établie, elle peut être utilisée en statistique inférentielle