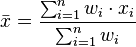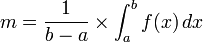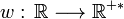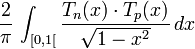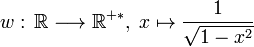Moyenne - Définition
Il y a plusieurs façon de calculer une moyenne d'un ensemble de nombres. Celle qu'il convient de retenir dépend de la grandeur physique que représentent ces nombres. Lorsque, dans le langage courant, on parle de moyenne, on évoque en fait la moyenne arithmétique.
Que représente la moyenne ?
La moyenne est la valeur unique que devraient avoir tous les individus d'une population (ou d'un échantillon) pour que leur total soit inchangé. Dans la plupart des cas, le total formé par les individus d'une population est la somme de leurs valeurs. La moyenne est alors la moyenne arithmétique. Mais si le total représenté par une population ou un échantillon n'est pas la somme de leurs valeurs, la moyenne pertinente ne sera plus la moyenne arithmétique. Si, par exemple, le total d'un ensemble d'individus est calculé par l'inverse de la somme des inverses (cas des vitesses d'un ensemble de fractions d'un trajet, par exemple), on doit calculer leur moyenne harmonique. Si, par exemple, le total d'un ensemble d'individus est le produit de leurs valeurs, il convient de calculer leur moyenne géométrique. On rencontre, en physique, de multiples moyennes : La capacité moyenne d'un ensemble de condensateurs en série est la moyenne harmonique de leurs capacités.
La moyenne ne peut donc se concevoir que pour une variable quantitative. On ne peut pas faire le total des valeurs d'une variable qualitative. Quand la variable est ordinale, on lui préférera la médiane.
La moyenne est beaucoup utilisée en évaluation scolaire. Dans de nombreux systèmes scolaires, une partie de l'évaluation des élèves débouche sur une note chiffrée, par exemple
- en France : de 0 à 10 ou de 0 à 20 (0 étant la plus mauvaise note, 10 ou 20 la meilleure) ;
- en Allemagne : de 6 à 1 (6 étant la plus mauvaise note, 1 la meilleure);
- au Canada : on utilise les pourcentages (%) de 0 à 100 % (100 étant la meilleure note et 0 la plus mauvaise).
On peut alors calculer la moyenne des notes d'une classe dans une matière, ou la moyenne des notes d'un élève dans une matière. Ces moyennes ont des sens différents :
- la moyenne de la classe est censée représenter un " niveau global ", si tant est que cela ait un sens ;
- dans le cas d'un examen de grande ampleur, comme par exemple le Baccalauréat, où de nombreux élèves passent la même épreuve mais sont corrigés par différents professeurs, la différence des moyennes entre les groupes peut indiquer une différence de correction selon le professeur (certains étant plus sévères, d'autres plus tolérants), et l'on peut par exemple effectuer une correction de notes, une " mise en adéquation ", afin que les groupes aient tous la même moyenne ; par exemple, si m1, m2… sont les moyennes des groupes et M la moyenne globale, alors les notes du groupe i seront multipliées par M/mi ;
- dans le cas d'un élève : la moyenne des notes sur une matière permet de niveler les résultats ; ainsi, si les résultats sont fluctuants, les faiblesses d'un moment sont rattrapées par les réussites d'un autre moment ;
- la moyenne des notes d'un élève dans plusieurs matières est une autre manière de niveler les résultats, non plus dans le temps mais selon la matière : les points forts rattrapent les points faibles ; la moyenne est alors un critère de sélection, sachant que ce que l'on demande d'un élève, ce n'est pas qu'il soit bon partout, mais qu'il ait des qualités permettant de rattraper ses défauts ; lorsque certaines matières sont plus importantes que d'autres, on applique des coefficients de pondération (cf. infra).
Dans ces exemples, la moyenne est un lissage des valeurs. On peut bien sûr se demander si la moyenne est un critère pertinent de sélection (voir Évaluation sommative) ; en général, ce n'est pas le seul critère qui entre en compte, à l'exception de certains examens et concours.
En physique, la moyenne correspond à la notion de barycentre. Lorsque l'on veut décrire le comportement de plusieurs objets, il est parfois possible de les remplacer par un objet fictif dont les propriétés (par exemple la position dans l'espace) sont la moyenne des propriétés des différents objets.
Lorsque les valeurs sont aléatoires, la moyenne est appelée " espérance ". Si l'on peut déterminer une loi statistique de cette variable aléatoire, l'espérance est en général un des paramètres fondamentaux de cette loi.
De manière générale, la moyenne n'est pas forcément une manière pertinente de représenter les données. On peut, par exemple, lui préférer la valeur médiane qui est la valeur à laquelle 50% des valeurs observées sont inférieures. La médiane n'est pas (sauf exception ou hasard) équivalente à la moyenne arithmétique de l'ensemble. En supposant que l'on ait, au préalable, rangé les valeurs observées de sorte qu'elles se trouvent indexées suivant l'ordre des valeurs croissantes
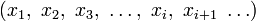
- pour un nombre pair 2n de valeurs, la médiane est la moyenne des deux valeurs centrales, soit (xn + xn + 1) / 2, ou toute autre valeur strictement comprise entre xn et xn + 1
- pour un nombre impair 2n+1 de valeurs, la médiane est unique et égale à xn + 1.
Moyenne arithmétique
La moyenne arithmétique est la moyenne ordinaire, c'est-à-dire la somme des valeurs numériques (de la liste) divisée par le nombre de ces valeurs numériques. Exemple: la hauteur moyenne des toits d'une rue.
Moyenne géométrique
La moyenne géométrique est définie de la manière suivante :
Il existe une relation entre la moyenne arithmétique et la moyenne géométrique,donnée par l'inégalité suivante:
-
-
-
-
-
-
-
-
-
-
![\frac{\sum_{i=1}^n a_i}{n}\ge\sqrt[n]{\prod_{i=1}^n a_i}](https://static.techno-science.net/illustration/Definitions/autres/1/105184563a9141279395bd0a0d2f4b5c_d0daa532714f55198fbb6a4754c2a09d.png)
-
-
-
-
-
-
-
-
-
On peut illustrer la moyenne géométrique avec les deux cas suivants :
- Si l'inflation d'un pays est de 5% la première année et de 15% la suivante, l'augmentation moyenne des prix se calcule grâce à la moyenne géométrique des coefficients multiplicateurs 1,05 et 1,15 soit une augmentation moyenne de 9,88% et non grâce à la moyenne arithmétique 10% (réponse intuitive).
- Le carré (c'est-à-dire le rectangle moyen à deux cotés égaux) qui a même surface (le total considéré ici) qu'un rectangle de cotés 3 et 7 a pour coté la moyenne géométrique des deux cotés du rectangle
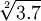
Il existe une moyenne géométrique pondérée, définie ci-dessous.
Étant donné en ensemble de données,
- X = { x1, x2, ..., xn}
ainsi que les poids correspondants,
- W = { w1, w2, ..., wn}
la moyenne géométrique pondérée est calculée comme étant:
Moyenne harmonique
La moyenne harmonique est définie de la manière suivante :
Si un train fait un trajet aller-retour entre 2 villes à la vitesse constante v1 pour l'aller et à la vitesse constante v2 au retour, la vitesse moyenne du trajet total n'est pas la moyenne arithmétique des 2 vitesses, mais bien leur moyenne harmonique.
Il existe une moyenne harmonique pondérée, définie ci-dessous.
Étant donné en ensemble de données,
- X = { x1, x2, ..., xn}
ainsi que les poids correspondants,
- W = { w1, w2, ..., wn}
la moyenne harmonique pondérée est calculée comme étant:
Moyenne quadratique
La moyenne quadratique est définie de la manière suivante :
Exemple: Si un rectangle a pour côtés 3 et 7, le carré (c'est-à-dire le rectangle moyen) qui a même diagonale (le total considéré ici) que ce rectangle, a pour côté la moyenne quadratique de 3 et 7, c'est-à-dire 5,3852.
Moyenne glissante
La moyenne glissante est une notion statistique, où la moyenne au lieu d'être calculée sur n valeurs fixes, est calculée sur n valeurs consécutives " glissantes ".
Ce type de calcul est aussi utilisé en informatique pour minimiser la taille mémoire nécessaire au stockage des valeurs intermédiaires. Différentes formules de moyennes glissantes existent, par exemple pour une moyenne glissante de période n :
-
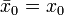
-
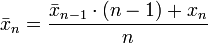
Cas général
La définition (et donc le calcul) des moyennes précédentes peut être synthétisée et généralisée à l'aide de la formule unique suivante :
où l'on retrouve :
- pour m = 1, la moyenne arithmétique
- pour m = 2, la moyenne quadratique
- pour m = -1, la moyenne harmonique
- lorsque m → 0, la limite de
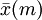
- lorsque m → +∞, la limite de
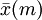
On peut faire le constat suivant, pouvant parfois aider dans le choix d'une moyenne :
- pour m = 1, toutes les valeurs de la série ont la même importance
- pour m > 1, les grandes valeurs sont privilégiées : plus l'on s'éloigne de 1 et plus l'on s'approche du maximum de la série
- pour m < 1, les faibles valeurs sont privilégiées.
Comparaison
Si a et b sont deux réels positifs tels que a < b, alors on a :
- a < Mharmonique(a,b) < Mgeometrique(a,b) < Marithmetique(a,b) < Mquadratique(a,b) < b
Pour démontrer ces comparaisons et les généraliser, on fait appel à la notion de fonction convexe.
Moyenne pondérée
La moyenne pondérée est utilisée, en géométrie pour localiser le barycentre d'un polygone, en physique pour déterminer le centre de gravité ou en statistique et probabilité pour calculer une espérance. On la calcule ainsi :
Dans le cas général le poids wi représente l'influence de l'élément xi par rapport aux autres.
A noter qu'il s'agit ici de la moyenne pondérée arithmétique. Il existe aussi des versions pondérées des autres moyennes, comme la moyenne géométrique pondérée et la moyenne harmonique pondérée.
Valeur moyenne d'une fonction
Pour toute fonction continue (ou même seulement continue par morceaux) sur un segment [a, b] non vide et non trivial (ie b > a), la valeur moyenne de ƒ sur [a, b] est le réel m défini par :
Cette notion généralise celle de moyenne d'un nombre fini de réels en l'appliquant à un nombre infini de valeurs prises par une fonction intégrable. Elle sert par exemple dans la décomposition en série de Fourier d'une fonction périodique : c'est la composante constante. En traitement du signal, pour les signaux périodiques, il s'agit de la composante continue (offset).
On peut aussi, par analogie avec les moyennes pondérées d'un nombre fini de réels, affecter " à chacune des valeurs prises par la fonction " un coefficient strictement positif. On utilise alors ce que l'on appelle une fonction poids
(w pour l'initiale de weight, poids en anglais) :
-
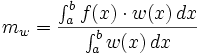
Ce procédé peut aussi s'utiliser sur un intervalle ouvert ou semi-ouvert mais borné (ie aucune de ses bornes n'est infinie) où la fonction ƒ×w est intégrable. On peut citer l'exemple classique servant à montrer l'orthogonalité de la famille des polynômes de Tchebychev :
où la fonction Tn×Tp est continue sur le fermé [0,1] et où la fonction poids est
est intégrable sur [0,1[, et dont l'intégrale vaut
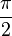
Nota : Lorsque la fonction est périodique de période T, elle a la même valeur moyenne sur toute période [a, a + T]. Cette valeur commune est appelée valeur moyenne de la fonction. Ainsi la fonction cosinus est de moyenne nulle, son carré de moyenne 1/2.
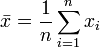
![\bar{x} = \sqrt[n]{\prod_{i=1}^n{x_i}}](https://static.techno-science.net/illustration/Definitions/autres/1/10a4a5b69d8b2cd60dd7423fb4a71b9a_f7884fc63840cabfcf5bc129881698f6.png)
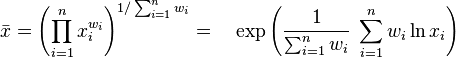
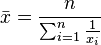
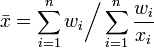
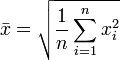
![\bar{x}(m) = \sqrt[m]{\frac{1}{n}\sum_{i=1}^n{x_i^m}}](https://static.techno-science.net/illustration/Definitions/autres/3/38347c662422aadda3a9f8180969fa59_75f0c1d67a48e3a6348943d1f2d5634c.png)