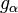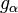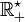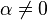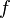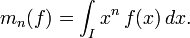Moment (mathématiques) - Définition
Notion de moment
La notion de moment en mathématiques, notamment en calcul des probabilités, a pour origine la notion de moment en physique.
Soit une fonction
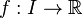
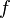
Remarque : pour un entier naturel n donné, l'ensemble des fonctions continues sur
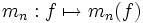
Problème des moments
On peut se demander si une fonction continue
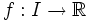
En d'autres termes : soient deux fonctions continues
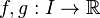
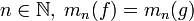
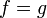
- D'après un théorème de Hausdorff, la réponse est affirmative lorsque
![[a,\, b]](https://static.techno-science.net/illustration/Definitions/autres/d/d2524b9940ce1c636bfb26ae09a941d2_de57359067f6b3298050b33ed863e8df.png)
![[a,\, b]](https://static.techno-science.net/illustrationWebp/Definitions/autres/d/d2524b9940ce1c636bfb26ae09a941d2_de57359067f6b3298050b33ed863e8df.png)
- Démonstration de ce théorème :
- La fonction
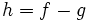
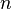
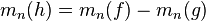
- On en déduit, par linéarité de l'intégrale, que
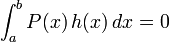
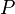
- en effet, si
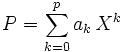
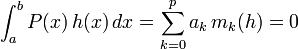
- Or, d'après un théorème de Weierstrass, pour toute fonction continue
![[a,\, b] \to \R](https://static.techno-science.net/illustration/Definitions/autres/8/8cc3f85cff4e3a1bba2863994946dad1_d90789c7bd1609fea1eb2f764e3379e9.png)
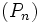
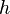
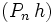
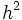
![\ [a,\, b]](https://static.techno-science.net/illustration/Definitions/autres/0/0451753e9f79fda12ee97e51cfc62d89_5ca360d2631ec2d91680c4996271a00f.png)
![\int_a^b [h(x)]^2\,dx = \lim_{n \to +\infty} \int_a^b P_n(x)\,h(x)\,dx = 0](https://static.techno-science.net/illustration/Definitions/autres/6/6d0d4bf8aaa69019e42e375be04dd86c_cfc0d0c490e59cc28b07ec2ff5c54061.png)
- Comme
![[a,\, b] \to \R](https://static.techno-science.net/illustrationWebp/Definitions/autres/8/8cc3f85cff4e3a1bba2863994946dad1_d90789c7bd1609fea1eb2f764e3379e9.png)
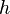
![\ [a,\, b]](https://static.techno-science.net/illustrationWebp/Definitions/autres/0/0451753e9f79fda12ee97e51cfc62d89_5ca360d2631ec2d91680c4996271a00f.png)
![\int_a^b [h(x)]^2\,dx = \lim_{n \to +\infty} \int_a^b P_n(x)\,h(x)\,dx = 0](https://static.techno-science.net/illustrationWebp/Definitions/autres/6/6d0d4bf8aaa69019e42e375be04dd86c_cfc0d0c490e59cc28b07ec2ff5c54061.png)
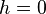
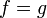
- Dans le cas général, la réponse est négative. Voici un contre-exemple probabiliste donné par William Feller. On considère la fonction
![\ f :\, ]0,\, +\infty[\, \to \R^+](https://static.techno-science.net/illustration/Definitions/autres/9/921a1a98c0e8a6f10020cc096551b8b1_5b14ac10c235a0d3a952a606e038063b.png)
![\ f :\, ]0,\, +\infty[\, \to \R^+](https://static.techno-science.net/illustrationWebp/Definitions/autres/9/921a1a98c0e8a6f10020cc096551b8b1_5b14ac10c235a0d3a952a606e038063b.png)
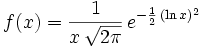
- On démontre (par changement de variable) que pour tout entier naturel
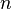
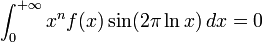
- Pour tout
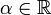
![\ g_\alpha :\, ]0,\, +\infty[\, \to \R](https://static.techno-science.net/illustration/Definitions/autres/0/06626d87d5163c9be842f7fff0e78fd7_02f7f16a4ae3e54c92e0daf5ac33debe.png)
![\ g_\alpha(x) = f(x)\, [1 + \alpha \sin(2 \pi \ln x)]](https://static.techno-science.net/illustration/Definitions/autres/8/8ec252f86cd1f9aa47d182b3e8fc2c08_cdc055883b32f78734422dc09f21ff86.png)
![\ g_\alpha :\, ]0,\, +\infty[\, \to \R](https://static.techno-science.net/illustrationWebp/Definitions/autres/0/06626d87d5163c9be842f7fff0e78fd7_02f7f16a4ae3e54c92e0daf5ac33debe.png)
![\ g_\alpha(x) = f(x)\, [1 + \alpha \sin(2 \pi \ln x)]](https://static.techno-science.net/illustrationWebp/Definitions/autres/8/8ec252f86cd1f9aa47d182b3e8fc2c08_cdc055883b32f78734422dc09f21ff86.png)
- Alors : quels que soient
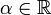
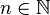
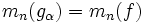
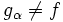
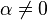
- Nota : pour tout
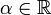
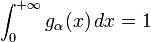
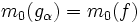
![\ \alpha \in [-1,\, +1]](https://static.techno-science.net/illustration/Definitions/autres/7/78bdde152a61dc9d677cb7e79085f373_450f3795798a5667c4ec41a8a75e444a.png)
![\ \alpha \in [-1,\, +1]](https://static.techno-science.net/illustrationWebp/Definitions/autres/7/78bdde152a61dc9d677cb7e79085f373_450f3795798a5667c4ec41a8a75e444a.png)
