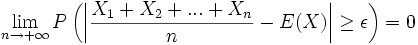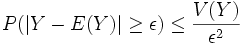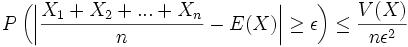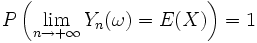Loi des grands nombres - Définition

La loi des grands nombres a été formalisée au XVII^e siècle lors de la découverte de nouveaux langages mathématiques.

Essentiellement, la loi des grands nombres indique que lorsque l'on fait un tirage aléatoire dans une série de grande taille, plus on augmente la taille de l'échantillon, plus les caractéristiques statistiques du tirage (l'échantillon) se rapprochent des caractéristiques statistiques de la population. Mais il est intéressant de noter que la taille de l'échantillon à prendre pour approcher les caractéristiques de la population initiale ne dépend que faiblement voire pas du tout de la taille de la série initiale : pour un sondage au Luxembourg ou aux États-Unis, il suffit, pour obtenir une précision égale de prendre un échantillon de même taille.

C'est sur cette loi que reposent la plupart des sondages ^[1]. Ils interrogent un nombre suffisamment important de personnes pour connaître l'opinion (probable) de la population entière. De même, sans la formalisation de la loi des grands nombres, l'assurance n'aurait jamais pu se développer avec un tel essor. En effet, cette loi permet aux assureurs de déterminer les probabilités que les sinistres dont ils sont garants se réaliseront ou non.

La loi des grands nombres sert aussi en statistique inférentielle, pour déterminer une loi de probabilité à partir d'une série d'expériences.

Les mathématiciens distinguent deux énoncés, appelés respectivement loi faible des grands nombres et loi forte des grands nombres.

Il est intéressant de noter que la loi des grands nombres soulève une question d'ordre métaphysique : personne ne s'étonne que des événements considérés de façon isolée soient soumis au hasard (il n'est pas impossible d'obtenir 1000 fois pile en lançant une pièce de monnaie 1000 fois...). Et pourtant, si l'on fait l'expérience, on constate qu'il n'y a pas de hasard global (en gros on obtient 50% de pile et 50% de face...), comme s'il existait une loi d'équilibre naturelle, comme si le chaos était impossible et les catastrophes improbables...

Il ne faut toutefois pas confondre la moyenne des gains et le gain absolu. Si deux joueurs jouent très longtemps à pile ou face, celui qui perd donnant un Euro à celui qui gagne, la moyenne des gains de chaque joueur tendra effectivement vers 0 (la moyenne étant définie comme : le gain divisé par le nombre de parties jouées), mais le gain de chaque joueur passera alternativement par des hauts et des bas d'amplitude croissante.

Loi faible des grands nombres

La loi faible des grands nombres est également appelée théorème de Khintchine (rarement utilisé).

Si l'on considère n variables aléatoires indépendantes qui suivent la même loi de probabilité, de variance finie et dont l'espérance est E(X), la loi faible des grands nombres stipule que, pour tout réel ε strictement positif, la probabilité que la moyenne empirique s'éloigne de l'espérance de plus de ε, tend vers 0 pour les grandes valeurs de n.

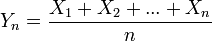
Elle se démontre en utilisant l'inégalité de Tchebychev :

Et en remarquant que la variable a pour espérance E(X) et pour variance donc

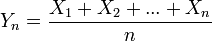
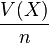
On dit aussi que Y_n converge en probabilité vers E(X)

Loi forte des grands nombres

Considèrons n variables aléatoires indépendantes qui suivent la même loi de probabilité, intégrables (i.e. ). En reprenant les notations ci-dessus, la loi forte des grands nombres précise que converge vers E(X) " presque sûrement ".

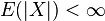
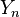
C’est-à-dire que :

Convergence vers une loi de probabilité

La même loi des grands nombres permet de dire que la répartition de la population de l'échantillon peut être approchée par la loi de probabilité de X pour n assez grand.

Pour prouver que la fréquence f_n(i) de la valeur x_i converge vers la probabilité p_i, il suffit d'utiliser la variable aléatoire qui prend la valeur 1 si X(ω) = x_i et la valeur 0 sinon.

Cette variable aléatoire a pour espérance p_i.

La fréquence f_n(i) converge alors en probabilité et aussi presque sûrement, vers p_i