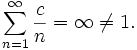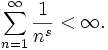Loi de Zipf - Définition

On nomme Loi de Zipf une observation empirique de la fréquence des mots dans un texte. Elle a pris le nom de son auteur, George Kingsley Zipf (1902-1950). Cette loi a été par la suite généralisée par Benoit Mandelbrot.

Genèse

Zipf avait entrepris d'analyser une œuvre monumentale de James Joyce, Ulysse, d'en compter les mots distincts, et de les présenter par ordre de nombre décroissants d'occurrences. La légende dit que

• le mot le plus courant revenait 8 000 fois ;
• le dixième mot 800 fois ;
• le centième, 80 fois ;
• et le millième, 8 fois.

Ces résultats semblent, à la lumière d'autres études que l'on peut faire en quelques minutes sur son PC, un peu trop beaux pour être strictement vrai — le dixième mot, dans une étude de ce genre, devrait apparaître dans les 1 000 fois, en raison d'un effet de coude observé dans ce genre de distribution. Reste que la loi de Zipf prévoit que dans un texte donné, la fréquence d'occurrence f(n) d'un mot est liée à son rang n dans l'ordre des fréquences par une loi du genre f(n) × n = K où K est une constante.

Point de vue théorique

Mathématiquement, il est impossible pour la version classique de la loi de Zipf de tenir exactement s'il existe une infinité de mots dans une langue, puisque pour toute constante de proportionnalité c > 0, la somme de toutes les fréquences relatives est proportionnelle à la série harmonique et doit être

Des études empiriques^{[réf. nécessaire]} ont trouvé qu'en anglais, les fréquences d'approximativement 1 000 mots les plus fréquemment utilisés sont approximativement proportionnels à où s est juste légèrement plus grand que 1.

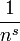
Tant que l'exposant s excède 1, il est possible pour une telle loi d'être vraie avec une infinité de mots, puisque si s > 1 alors

La valeur de cette somme est , où ζ est la fonction Zeta de Riemann.

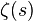
On sait toutefois que le nombre de mots d'une langue est limité. Le vocabulaire d'un enfant de 10 ans tourne autour de 5 000 mots, celui d'un adulte cultivé de 70 000,et les dictionnaires en plusieurs volumes peuvent monter de 130 000 à 200 000.

Un cas particulier d'une loi générale

Benoît Mandelbrot démontra dans les années 1950 qu'une loi similaire à celle de Zipf pouvait se déduire de deux considérations liées à la théorie de l'information de Claude Shannon.

Loi statique de Shannon

Selon la loi statique, le coût de représentation d'une information augmente comme le logarithme du nombre des informations à considérer.

Il faut par exemple 5 bits pour représenter des nombres de 0 à 31, mais 16 pour des nombres de 0 à 65535. De même, on peut former 17576 sigles de 3 lettres, mais 456976 de 4 lettres, etc.

Loi dynamique de Shannon

La loi dynamique indique comment maximiser l'utilité d'un canal par maximisation de l'entropie en utilisant prioritairement les symboles les moins coûteux (ainsi en code Morse le e, lettre fréquente, est codé par un simple point (.) tandis que le x, lettre plus rare, se représente par un trait point point trait (-..-). Le codage de Huffman met en application cette loi dynamique.

La synthèse de Mandelbrot

Mandelbrot émet l'hypothèse audacieuse que le coût d'utilisation est directement proportionnel au coût de stockage, ce qu'il constate est vrai sur tous les dispositifs qu'il a observés, de l'écriture comptable jusqu'aux ordinateurs.

Il élimine donc le coût entre les deux équations et se retrouve avec une famille d'équations liant nécessairement la fréquence d'un mot à son rang si l'on veut que le canal soit utilisé de façon optimale. C'est la loi de Mandelbrot, dont celle de Zipf ne représente qu'un cas particulier, et qui est donnée par la loi :

où K est une constante.

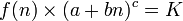
la loi se ramenant à celle de Zipf dans le cas particulier où a vaudrait 0, b et c tous deux 1, cas qui ne se rencontre pas dans la pratique. Dans la plupart des langues existantes, c est voisin de 1,1 ou 1,2, et proche de 1,6 dans le langage des enfants^[1].

Les lois de Zipf et de Mandelbrot prennent un aspect spectaculaire si on les trace selon un systèmes de coordonnées log-log : la loi de Zipf correspond alors à une belle droite, et celle de Mandelbrot à la même chose avec une bosse caractéristique. Cette bosse se retrouve précisément dans les textes littéraires disponibles sur le Net, analysables en quelques minutes sur ordinateur domestique avec des langages comme le Python. La courbe fournie ici représente le logarithme décimal du nombre d'occurrences des termes d'un forum du Web tracé en fonction du logarithme décimal du rang de ces mots.

• On constate que le mot le plus fréquent y apparaît un peu plus de 100 000 fois (10⁵).
• La taille du vocabulaire effectivement utilisé (il serait plus exact de parler de la taille de l'ensemble des formes fléchies) est de l'ordre de 60 000 (#10^4.7).
• L'aspect linéaire de Zipf y apparaît clairement, bien que le coude caractéristique expliqué par Mandelbrot n'y soit que léger. On notera aussi que la pente n'est pas exactement de −1 comme le voudrait la loi de Zipf.
• L'intersection projetée de cette courbe avec l'axe des abscisses fournirait à partir d'un texte de taille limitée (quelques pages A4 dactylographiées) une estimation de l'étendue du vocabulaire d'un scripteur.
  • On peut remarquer que nous nous livrons déjà subjectivement à la même estimation en lisant quelques pages d'un écrivain que nous ne connaissons pas, et que c'est ce qui nous permet en feuilletant un ouvrage de savoir si ce vocabulaire est en adéquation avec le nôtre.
  • On peut remarquer aussi que la répétition de mots se voulant savants comme extemporanément ou hiératique ne fera pas illusion, puisque c'est la répétition elle-même qui constitue l'indice de pauvreté du vocabulaire et non les mots utilisés eux-mêmes.

Similarité

Le rapport entre lois de Zipf et de Mandelbrot d'une part, entre lois de Mariotte et de van der Waals d'autre part est similaire : on a dans les premiers cas une loi de type hyperbolique, dans les secondes une légère correction rendant compte de l'écart entre ce qui était prévu et ce qui est observé, et proposant une justification. Dans les deux cas, un élément de correction est l'introduction d'une constante manifestant quelque chose d'" incompressible " (chez Mandelbrot, le terme a).

Une loi à utiliser avec prudence

Il est tentant chaque fois que l'on voit des informations classées par ordre décroissant de se dire : " Elles doivent suivre une loi de Zipf ". Sans que ce soit nécessairement faux, il serait dangereux de le considérer comme allant de soi. Si nous prenons par exemple 100 entiers aléatoires entre 1 et 10 selon une loi uniforme, que nous les regroupons et que nous trions le nombre d'occurrences de chacun, nous obtenons la courbe ci-contre.

On admettra que si l'on se fie juste à une première impression visuelle, cette courbe paraît très " zipfienne ", alors que c'est un tout autre modèle qui a engendré la série des données. Or il n'est pas possible de faire commodément un Chi2 sur la loi de Zipf, le tri des valeurs venant faire obstacle à l'usage d'un modèle probabiliste classique (n'oublions pas en effet que la répartition des occurrences n'est pas celle des probabilités d'occurrences, et que cela peut conduire à beaucoup d'inversions dans les tris).

La famille de distributions de Mandelbrot est certes démontrée adéquate de façon formelle pour un langage humain sous ses hypothèses de départ concernant le coût de stockage et le coût d'utilisation, qui découlent elles-mêmes de la théorie de l'information. En revanche il n'est pas prouvé qu'utiliser la loi de Zipf comme modèle pour la distribution des populations des agglomérations d'un pays soit un modèle pertinent — bien que le contraire ne soit pas prouvé non plus.

Ajoutons que l'estimation des paramètres de Mandelbrot à partir d'une série de données pose également problème, et fait encore aujourd'hui l'objet de débats^{[réf. nécessaire]}. Il ne saurait être question par exemple d'utiliser une méthode de moindres carrés sur une courbe en log-log dont de surcroit le poids des points est loin d'être comparable. Mandelbrot lui-même a fini par se désintéresser de la question^{[réf. nécessaire]}.