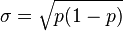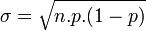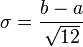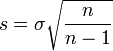Écart type - Définition

En mathématiques, l'écart type est une quantité réelle positive, éventuellement infinie, utilisée dans le domaine des probabilités pour caractériser la répartition d'une variable aléatoire autour de sa moyenne. En particulier, la moyenne et l'écart type caractérisent entièrement les lois gaussiennes à un paramètre réel, de sorte qu'ils sont utilisés pour les paramétrer. Plus généralement, l'écart type, à travers son carré appelé variance , permet de caractériser des lois gaussiennes en dimension supérieure. Ces considérations ne sont pas sans importance, notamment dans l'application du théorème central limite.

En statistiques, l'écart type ou déviation standard est défini au contraire pour un ensemble fini de données numériques interprétées comme la réalisation d'une variable aléatoire. Il est alors utilisé pour mettre en place des tests, autrement dit, il permet de décider si une probabilité est plausible compte tenu des valeurs disposées avec une certaine marge d'erreur. L'écart type est aussi utilisé dans les problèmes de régression linéaire.

Les écarts types connaissent de nombreuses applications, tant dans les sondages, qu'en physique, ou en biologie. Ils permettent en pratique de rendre compte des résultats numériques d'une expérience répétée.

Définition

Dans la formulation moderne des probabilités, suite aux travaux de Henri Lebesgue, une variable aléatoire X est une application à valeurs réelles ou vectorielles, dépendant d'un paramètre x suivant une loi de probabilité P. Si la compréhension du formalisme fait appel à la théorie de la mesure, son utilisation reste simple. L'application X ne joue pas un rôle fondamental ; seule sa loi, l'image de P par X, notée P_X, importe. Il s'agit d'une mesure sur R ou sur Rⁿ. Deux quantités lui sont associées :

• Sa moyenne, notée E[X], aussi appelée espérance :
• Son écart type, généralement noté σ_X, défini comme la racine carrée de l'espérance de (X-E[X])² :

.

Ici, l'élévation au carré pour le membre de droite désigne implicitement la norme euclidienne au carré dans le cas où X est à valeurs vectorielles.

Cette identité se spécialise dans un grand nombre de cas particuliers. Entre autres :

Probabilité discrète

Si la variable X prend un nombre fini de valeurs réelles x₁, ..., x_n, avec des probabilités respectives p₁, ..., p_n (sous la condition ), l'écart type est donnée par :

, où : .

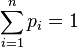
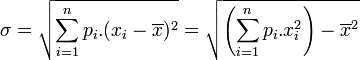
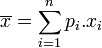
En particulier, si la loi de X est uniforme sur un ensemble fini de valeurs, on a :

, où : .

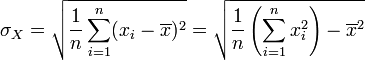
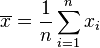
Ces formules se généralisent immédiatement en dimension supérieure en remplaçant l'élévation au carré par la norme euclidienne au carré.

Probabilité uniformément continue

La loi P_X est dite uniformément continue lorsque la probabilité que X appartienne au segment [a,b] est :

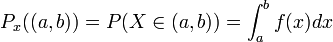
où f est une fonction localement intégrable pour la mesure de Lebesgue, par exemple mais pas nécessairement une fonction continue. Cette fonction f s'appelle la densité de la loi P_X. Elle est globalement intégrable et de carré intégrable.

L'écart type de X est défini par :

.

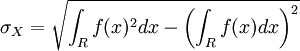
Exemples d'écart types

Le tableau suivant donne les écarts types pour les lois couramment rencontrées :

Nom de la loi	Paramètre	Description	Ecart type
Loi de Bernoulli	p	Loi discrète de valeurs 0 avec probabilité 1-p et 1 avec probabilité p
Loi binomiale	p et n>1	Loi de la somme indépendantes de n variables suivant la loi de Bernouilli de paramètre p
Loi géométrique	p	Loi discrète sur N telle que la probabilité d'obtenir l'entier n soit (1-p).pn	σ = p / (1 − p)2
Loi uniforme sur un segment	a<b	Loi uniformément continue sur R de densité la fonction indicatrice de [a,b] à un coefficient près
Loi exponentielle	p	Loi uniformément continue de support R+ de densité la fonction f(x)=p.exp(-p.x)	σ = 1 / p

En théorie des sondages

Lorsqu'il s'agit d'estimer la dispersion autour de la moyenne d'un caractère statistique dans une population de grande taille à partir d'un échantillon de taille n, on utilise pour l'écart type la valeur suivante

.

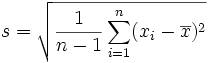
On peut remarquer que

Pourquoi n - 1 ?

La question que l'on se pose généralement est " Pourquoi n - 1 ? ". La raison pour laquelle on divise par n - 1 au lieu de n est un bel exemple de l'interaction permanente entre les statistiques et les probabilités.

Le sondage de n individus correspond à une série de n variables aléatoires x_i indépendantes d'espérance E(X) et de variance V(X).

La moyenne de l'échantillon est une variable aléatoire d'espérance E(X) et de variance (la moyenne de n variables aléatoires fluctue moins qu'une seule variable aléatoire).

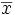
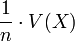
La variance v de l'échantillon est une variable aléatoire dont on veut calculer l'espérance.

.

est une variable aléatoire d'espérance donc égale à E(X)² + V(X).

est une variable aléatoire d'espérance E(X)² + V(X).

est une variable aléatoire d'espérance .

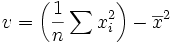
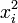
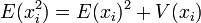
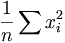
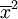
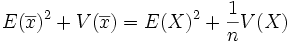
Donc .

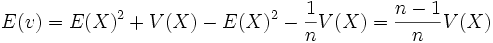
La variance v de l'échantillon fluctue donc autour de et non autour de V(X) comme on aurait pu s'y attendre.

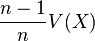
Pour obtenir une estimation de V(X), il est donc nécessaire de prendre . On pourrait dire que v est un estimateur biaisé.

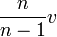
Et pour obtenir une estimation de l'écart type σ(X), il est nécessaire de prendre .

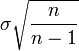
Aspect qualitatif

Plus communément appelée écart type, la déviation standard caractérise la largeur de la distribution. Elle est exprimée mathématiquement comme étant la racine carrée de la variance, celle-ci mesurant la distribution des valeurs autour du centre de la courbe.

Écart type (S) = Racine carrée de la variance

• L'écart type est la mesure de dispersion, ou étalement, la plus couramment utilisée en statistique lorsqu'on emploie la moyenne pour calculer une tendance centrale. Il mesure donc la dispersion autour de la moyenne. En raison de ses liens étroits avec la moyenne, l'écart type peut être grandement influencé si cette dernière donne une mauvaise mesure de tendance centrale.
  

• Contrairement à l'étendue et aux quartiles, la variance permet de combiner toutes les valeurs à l'intérieur d'un ensemble de données afin d'obtenir la mesure de dispersion. La variance (symbolisée par S²) et l'écart type (la racine carrée de la variance, symbolisée par S) sont les mesures de dispersion les plus couramment utilisées.
  

La variance est définie comme étant la moyenne arithmétique des carrés des différences entre les valeurs observées et la moyenne. C'est une mesure du degré de dispersion d'un ensemble de données. On la calcule sous la forme de l'écart au carré moyen de chaque nombre par rapport à la moyenne d'un ensemble de données.

Répartition de la population

Lorsque la variable étudiée est gaussienne (répartition selon une courbe en cloche), l'écart type permet de déterminer la répartition de la population autour de la valeur moyenne.

Par exemple : Si par convention, la déviation standard par rapport à un échantillon équivaut à 15 points de QI de différence, cela signifie que les 2/3 environ de la population d'une classe d'âge ont un QI compris entre 85 et 115. Voir également à ce sujet l'intervalle de confiance d'une distribution normale gaussienne.

Interprétation d'un écart type élevé

Généralement, plus les valeurs sont largement distribuées, plus l'écart type est élevé. Imaginez, par exemple, que nous devions séparer deux ensembles différents de résultats d'examens de 30 élèves; les notes du premier examen varient de 31 % à 98 % et celles du second, de 82 % à 93 %. Compte tenu de ces étendues, l'écart type serait plus grand pour les résultats du premier examen.

Cependant, il n'est pas toujours facile d'évaluer l'importance que doit avoir l'écart type pour que les données soient largement dispersées.
L'importance de l'écart type dépend aussi de l'importance de la valeur moyenne de l'ensemble des données. Lorsque vous mesurez quelque chose en millions, le fait d'avoir des mesures qui se rapprochent de la valeur moyenne n'a pas la même signification que si vous mesurez le poids de deux personnes.
Par exemple, si après avoir mesuré les recettes annuelles de deux grandes entreprises, vous constatez un écart de 100 000 euros, la différence est considérée comme étant peu significative, alors que si vous mesurez le poids de deux personnes, dont l'écart est de 30 kilogrammes, la différence est considérée comme étant très significative.
Voilà pourquoi il est parfois utile de travailler, dans certains cas, sur l'écart type relatif (écart type quotienté par la moyenne).

On nomme variance le carré de l'écart type : V(X) = σ²