Droite de Henry - Définition
La droite de Henry est une méthode pour visualiser les chances qu'a une distribution d'être gaussienne. Elle permet de lire rapidement la moyenne et l'écart type d'une telle distribution.
Principe
Si X est une variable gaussienne de moyenne
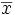
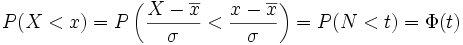
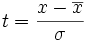
(on note Φ la fonction de répartition de la loi normale centrée réduite).
Pour chaque valeur xi de la variable X, on peut (à l'aide d'une table de la fonction Φ) :
- calculer P(X < xi)
- en déduire ti tel que Φ(ti) = P(X < xi)
Si la variable est gaussienne, les points de coordonnées (xi ; ti) sont alignés sur la droite d'équation
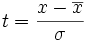
Exemple numérique
Lors d'un examen noté sur 20, on obtient les résultats suivants :
- 10% des candidats ont obtenu moins de 4
- 30% des candidats ont obtenu moins de 8
- 60% des candidats ont obtenu moins de 12
- 80% des candidats ont obtenu moins de 16
On cherche à déterminer si la distribution des notes est gaussienne, et, si oui, ce que valent son espérance et son écart type.
On connaît donc 4 valeurs xi, et, pour ces 4 valeurs, on connaît P(X < xi).
En utilisant la table wikisource : Table de la fonction de répartition de la loi normale centrée réduite, on détermine les ti correspondants :
| xi | P(X<xi) = Φ(ti) | ti |
| 4 | 0,10 | -1,28 |
| 8 | 0,30 | -0,525 |
| 12 | 0,60 | 0,255 |
| 16 | 0,80 | 0,84 |
Il suffit alors de tracer les points de coordonnées (xi ; ti).
Les points paraissent alignés ; la droite coupe l'axe des abscisses au point d'abscisse 11 et le coefficient directeur est (0,84 +1,28)/12 environ, ce qui donnerait un écart type de 12/2,12 = 5,7.
Cela laisse penser que la distribution est gaussienne de paramètres m, σ2, où m = 11 et σ = 5,7.

















































