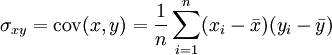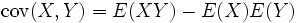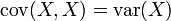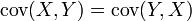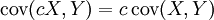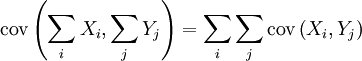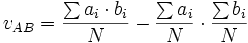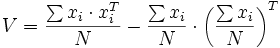Covariance - Définition
Pour le principe physique, voir Principe de covariance générale.
En statistiques, la covariance est une méthode mathématique permettant d'évaluer le sens de variation de deux variables et, par là, de qualifier l'indépendance de ces variables.
Définition
En théorie des probabilités et en statistique, on nomme covariance de deux variables aléatoires à valeurs réelles X et Y la valeur :
avec
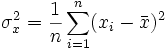
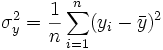
Intuitivement, la covariance est une mesure de la variation simultanée de deux variables aléatoires. C'est-à-dire que la covariance devient plus positive pour chaque couple de valeurs qui diffèrent de leur moyenne dans le même sens, et plus négative pour chaque couple de valeurs qui diffèrent de leur moyenne dans le sens opposé.
L'unité de mesure de la covariance cov(X,Y) est le produit de l'unité des variables aléatoires X et Y. En revanche, la corrélation, qui dépend de la covariance, est une mesure de dépendance linéaire sans unité.
La définition ci-dessus est équivalente à la formule suivante, plus souvent utilisée pour les calculs :
où E désigne l'espérance mathématique. Si X et Y sont des variables indépendantes, alors leur covariance est nulle. En effet, on a alors :
-
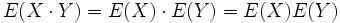
La réciproque, cependant, n'est pas vraie. Il est en effet possible que X et Y ne soient pas indépendantes, et que leur covariance soit nulle. Des variables aléatoires dont la covariance est nulle sont dites non corrélées.
Si X et Y sont des variables aléatoires à valeurs réelles, et c une constante (" constante ", dans ce contexte, signifiant non-aléatoire), alors les formules suivantes sont des conséquences directes de la définition de la covariance :
Exemple
Dans un forum Internet, quelqu'un affirme que les activités sont plus intenses les jours de pleine lune. On peut ne pas disposer du calendrier des pleines lunes, mais si cette affirmation est exacte et si l'on nomme N(t) le nombre de contributions au jour t, la covariance entre N(t) et N(t+28) cumulée sur toutes les valeurs de t sera supérieure en principe aux covariances entre N(t) et N(t+x) pour les valeurs de x différentes de 28.
Résultats
On constate en effet un pic léger de covariance pour la valeur 28. La théorie de l'influence de la pleine lune est-elle vérifiée ?
Examen plus détaillé
La courbe de covariance montre en effet un léger pic pour la valeur 28, mais d'autres pics d'importance croissante pour 21, 14 et 7. Il est donc plus plausible d'émettre l'hypothèse d'une pointe d'activité hebdomadaire (week-end, par exemple) pour ce forum, en tant que variable explicative (ce cas a été observé en 1995 sur le forum Compuserve du journal Le Monde).
Détails techniques
La covariance vAB de deux variables aléatoires A et B observées conjointement N fois est définie par:
La matrice de covariance V d'une variable aléatoire vectorielle X observée N fois est définie par:
On remarquera que si A est la variable aléatoire correspondant à la a-ième coordonnée de X et si B est la variable aléatoire correspondant à la b-ième coordonnée de X alors on a vAB = Vab.
L'inverse de la matrice de covariance est parfois désignée par le terme de " matrice de précision ".
Bilinéarité
Soient X et Y deux variables aléatoires définies sur le même espace probabilisé. La formule var(X+Y) = var(X) + var(Y) + 2cov(X,Y) est l'analogue de (x + y)2 = x2 + y2 + 2xy. En fait, la plupart des propriétés de la covariance sont analogues à celles du produit de deux réels ou du produit scalaire de deux vecteurs.
Usage
La connaissance des covariances est le plus souvent indispensable dans les fonctions d'estimation, de filtrage et de lissage. Elles permettent, entre autres en photographie, d'arriver à corriger de façon spectaculaire les flous de mise au point ainsi que les flous de bougé, ce qui est extrêmement important pour les clichés astronomiques. On les utilise également en automatique. En sociolinguistique, la covariance désigne la correspondance entre l’appartenance à une certaine classe sociale et un certain parler inhérent à cette condition sociale.