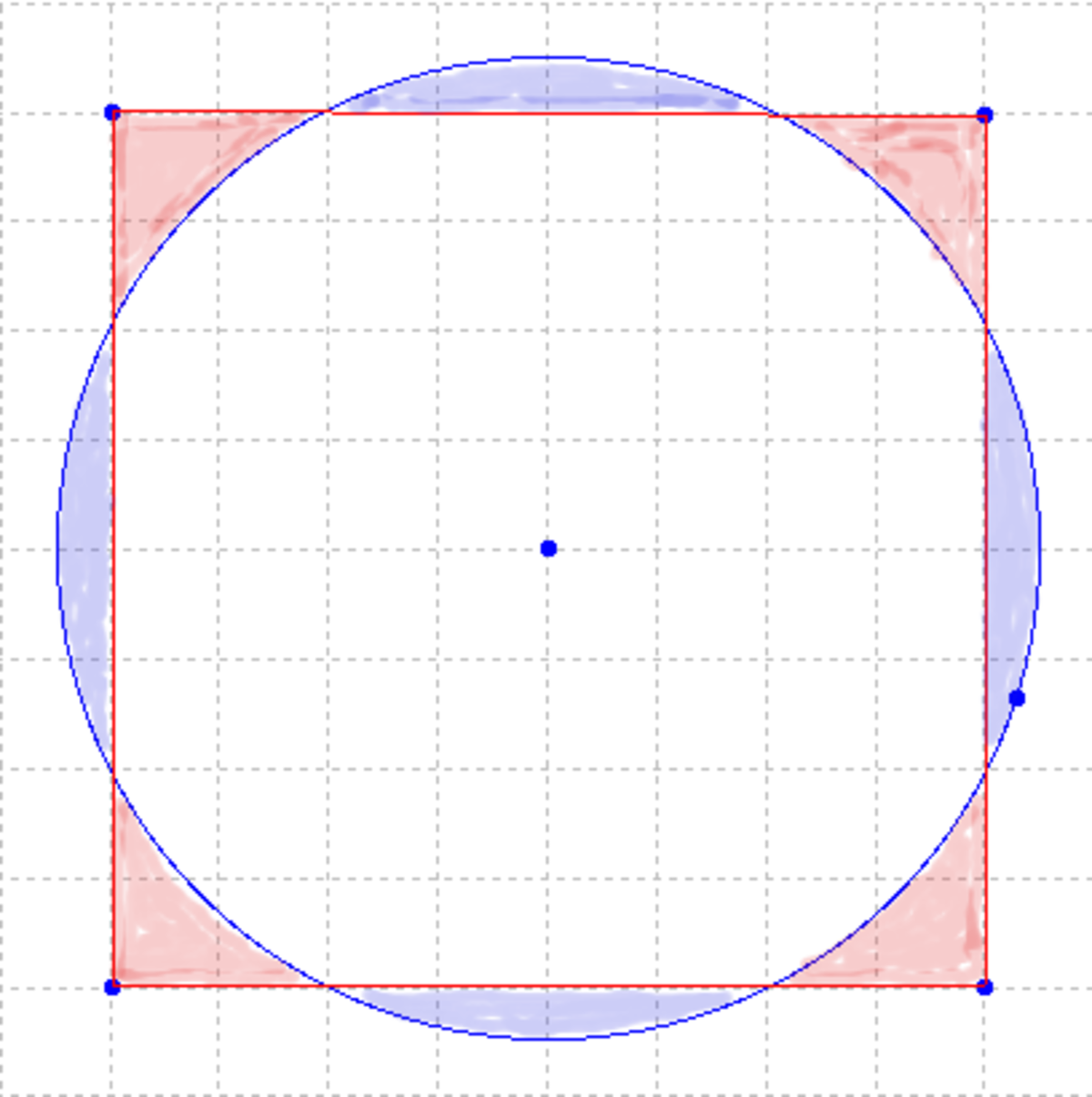
Quadrature du cercle - Définition
La quadrature du cercle est un problème classique de mathématiques apparaissant en géométrie. Il fait partie des trois grands problèmes de l'Antiquité, avec la trisection de l'angle et la duplication du cube. Dans le plus ancien texte mathématique retrouvé, le Papyrus Rhind (~1650 av. J.-C.), le scribe Ahmès proposait déjà une solution approchée du problème. Le premier scientifique grec à s'intéresser à la question a été Anaxagore de Clazomènes.
Le problème est de construire un carré de même aire qu'un cercle donné à l'aide d'une règle et d'un compas (voir nombre constructible). Il remonte à l'invention de la géométrie et a occupé de nombreux mathématiciens aux cours des siècles. Grégoire de Saint-Vincent était passionné par le problème: il écrivit un ouvrage de 1000 pages estimant - erronément - l'avoir résolu. C'est en 1837 que Pierre-Laurent Wantzel démontre un théorème qui permet d'exhiber la forme des équations des problèmes impossibles à résoudre à la règle et au compas. Mais il faudra attendre jusqu'en 1882 pour que le mathématicien allemand Ferdinand von Lindemann démontre la transcendance de π pour appliquer le théorème de Wantzel au problème de la quadrature du cercle et ainsi démontrer qu'elle était impossible à réaliser. L'Académie des sciences, qui avait déjà pressenti ce résultat un siècle auparavant, n'acceptait plus de " preuve " de cette quadrature depuis 1775.
C'est la limitation des outils à utiliser qui rend ce problème impossible. En autorisant un outil permettant de créer une spirale d'Archimède, le problème devient possible.
Une solution de construction demande la construction de la racine carrée de π,
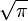
Ce problème est resté populaire et de nombreux quadrateurs amateurs envoient encore aujourd'hui de fausses preuves aux académies scientifiques.
Métaphore
Chercher la quadrature du cercle est une expression désignant un problème insurmontable.