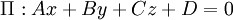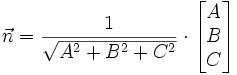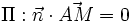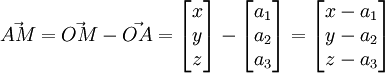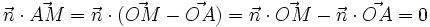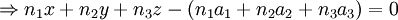Plan (mathématiques) - Définition
En mathématiques, un plan est un objet fondamental à deux dimensions. Intuitivement il peut être visualisé comme une feuille d'épaisseur nulle qui s'étend à l'infini. L'essentiel du travail fondamental en géométrie et en trigonométrie s'effectue en deux dimensions donc dans un plan.
Définitions
Dans les Éléments d'Euclide, seule la notion de figure plane est définie. Une figure plane est une figure contenue dans la surface balayée par une droite dont un point est fixé et le second assujetti à se déplacer sur une seconde droite[1]. Cette définition repose malheureusement sur la définition donnée de surface qui manquait de précision. Dans la présentation actuelle des mathématiques, un plan vectoriel ou affine est défini comme un objet de l'algèbre linéaire :
-
- Un Plan (vectoriel ou affine) est un K-espace vectoriel ou un K-espace affine de dimension deux, où K désigne un corps.
Le cas le plus fréquent correspond à celui ou le corps K est celui des nombres réels. Ainsi le plan complexe désigne le corps des nombres complexes considéré comme un espace vectoriel de dimension deux sur le corps des réels.
Un cas important est celui où un plan désigne un sous-espace affine de dimension deux dans un espace de dimension trois sur le corps des réels. Cette situation modèlise simplement notre géométrie.
Il existe alors de nombreuses manières de définir un plan, notamment :
- Le plus petit espace affine contenant trois points distincts et non alignés;
- Le plus petit espace affine contenant une droite et un point n'appartenant pas à cette droite;
- Le plus petit espace affine contenant deux droites non confondues et sécantes;
- Le plus petit espace affine contenant deux droites non confondues et parallèles;
- Le plus petit espace affine contenant un point et un vecteur normal;
- Le plus petit espace affine contenant un point et deux vecteurs non colinéaires.
Par la suite, nous utiliserons les deux dernières définitions pour l'élaboration des équations du plan.
Positions relatives de deux plans
Dans un espace en trois dimensions, il n'existe que deux positions relatives de deux plans :
- parallèles : strictement (intersection vide) ou bien confondus;
- sécants : leur intersection est alors une droite. Ils peuvent être orthogonaux (une droite de l'un est orthogonale à deux droites sécantes de l'autre).
Positions relatives d'un plan et d'une droite
Dans un espace en trois dimensions, il n'existe que deux positions relatives d'un plan et d'une droite :
- parallèles : leur intersection est soit vide, soit la droite tout entière (droite incluse dans le plan);
- sécants : leur intersection est un point.
Équations dans un espace de dimension trois
Définition par deux vecteurs et un point
Soit un point
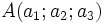
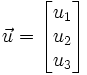
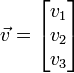
Combinaison linéaire
Le plan passant par A, de vecteurs directeurs
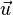
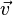
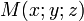

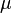
-
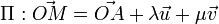
ou
-
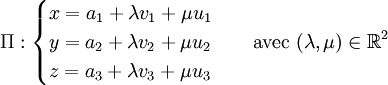
Coplanarité
Soit
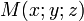
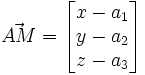
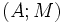
Pour que ces trois vecteurs soient coplanaires, il faut que leur produit mixte soit nul :
En mettant en évidence les termes :
On distingue 4 parties, 4 nombres que nous appellerons A,B,C,D. Nous pouvons ainsi écrire l'équation cartésienne du plan :
Nous remarquons en outre que les nombres A,B et C sont les composantes du vecteur
Définition par un vecteur normal et un point
Orthogonalité
Le plan passant par
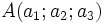
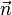
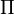
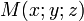
avec
Cette définition amène ainsi à l'équation cartésienne :
On identifie généralement le quadruplet
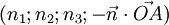
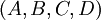
![(\vec{AM} \times \vec u) \cdot \vec v = [\vec{AM},\vec u,\vec v] = 0](https://static.techno-science.net/illustration/Definitions/autres/e/eebe5c75b8d7b5c68cb86a72eb883090_6f0a0deecfb4d8635ef8f2a3e8817ae8.png)
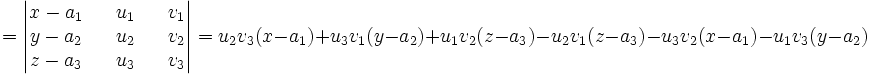
![[\vec{AM},\vec u,\vec v] = (u_2v_3 - u_3v_2)x\quad +\quad (u_3v_1 - u_1v_3)y\quad +\quad (u_1v_2 - u_2v_1)z\quad -\ u_2v_3a_1 - u_3v_1a_2 - u_1v_2a_3 + u_2v_1a_3 + u_3v_2a_1 + u_1v_3a_2\,](https://static.techno-science.net/illustration/Definitions/autres/5/5ecf8d05000d04dc45b0a9b356c9e45b_0bff953450af1e5fc91c12589559d71b.png)