Losange - Définition

Dans un espace affine normé, un losange est un parallélogramme ayant deux côtés consécutifs de même longueur.

Propriétés

Pour tout quadrilatère d'un plan affine euclidien (espace affine euclidien de dimension 2) les propositions suivantes sont équivalentes :

1. Le quadrilatère est un losange.
2. Le quadrilatère a ses quatre côtés de même longueur.
3. Le quadrilatère est un parallélogramme et ses diagonales sont perpendiculaires.

Ces équivalences sont cependant en défaut dans le cas d'un losange aplati (le point 3 n'a alors pas de sens) :

Preuve

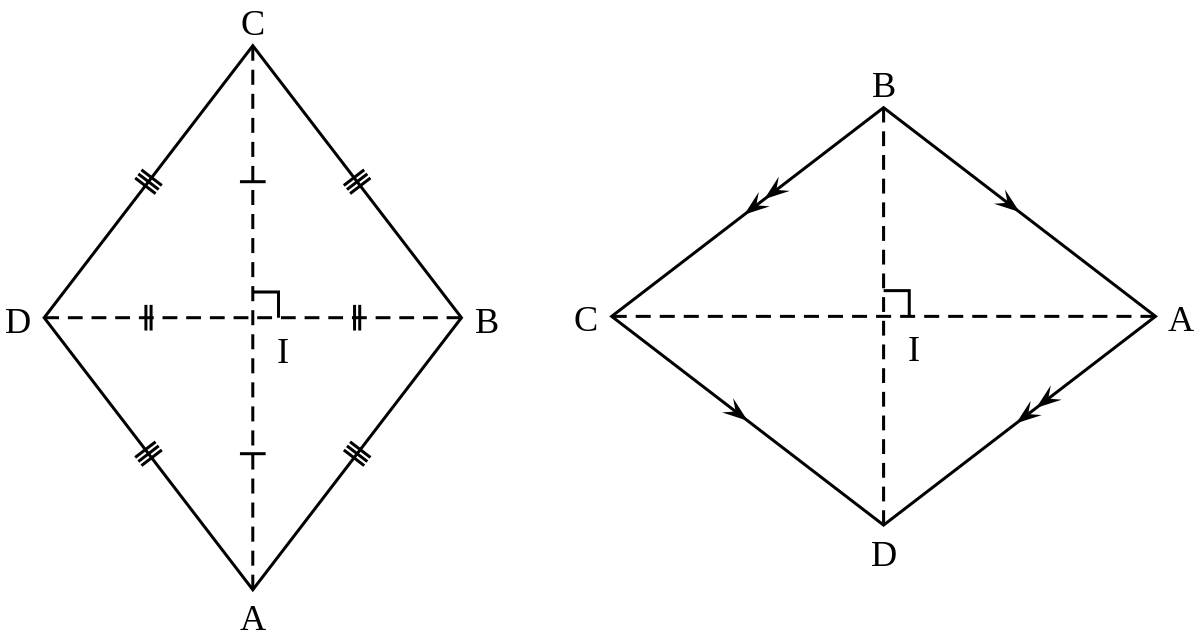
Soit ABCD un quadrilatère. Soit I le milieu de [AC] et J le milieu de [BD].

Comme A C on peut parler de la médiatrice d_AC de [AC]. Comme B D on peut parler de la médiatrice d_BD de [BD].

Montrons (1) implique (2) :

On suppose que ABCD est un losange.

Comme c'est un parallélogramme, on a AB = CD, BC = AD et comme c'est un losange, on a AB = CB. Par transitivité, AB = BC = CD = DA.

Montrons (2) implique (3) :

On suppose que AB = BC = CD = DA.

De AB = BC et CD = DA, on conclut (DB) = d_AC. Ainsi (DB) est perpendiculaire à (AC) et I appartient à (DB) et (AC).

De BC = CD, on conclut que .

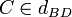
On a et donc . Comme d_BD et (AC) ont le point C en commun, on conclut que d_BD = (AC) et donc que J appartient à (AC) et (BD).

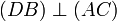
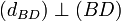
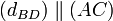
Comme (AC) et (BD) sont perpendiculaires, elles ont un unique point commun et donc I = J. ABCD a ses diagonales qui se coupent en leur milieu, c'est donc un parallélogramme.

Montrons (3) implique (1) :

On suppose que (AC) et (BD) sont perpendiculaires et que ABCD est un parallélogramme. Comme (AC) est perpendiculaire à (BD) et passe par J, on conclut que (AC) = d_BD et donc que CB = CD.

Remarque

La définition du losange comme étant un parallélogramme impose qu'un losange est une figure plane. Il existe des quadrilatères (avec quatre sommets bien distincts) ayant les quatre côtés de même longueur qui ne sont pas des losanges. Il suffit de se placer dans un espace affine euclidien de dimension 3 et de faire subir à un côté d'un "vrai losange" une rotation suivant l'une des ses diagonales.

Aire

Si a et b sont les longueurs des diagonales, alors l'aire du losange est :

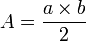
en effet, les diagonales définissent quatre triangles rectangles qu'il suffit de réagencer pour avoir un rectangle dont les côtés sont a/2 et b (par exemple) ; on applique alors la formule donnant l'aire du rectangle.

Rhomboèdre

Un rhomboèdre est un polyèdre dont les six faces sont des losanges.

Anecdote

" Le Losange " ou " la marque au losange " sont des expressions régulièrement utilisées pour désigner la marque automobile Renault, par analogie à la forme de son logo.