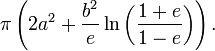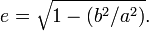Sphéroïde - Définition
Un sphéroïde ou ellipsoïde de rotation est une surface quadrique en 3 dimensions obtenue par rotation d'une ellipse autour d'un de ses axes principaux. Si l'ellipse tourne autour de son axe principal, la surface est appelée un sphéroïde prolate (similaire à la forme d'un ballon de rugby). Si l'axe secondaire est choisi, la surface est appelée un sphéroïde oblate (similaire à la forme de la Terre).
|

|
La sphère est un cas particulier de la sphéroïde dans laquelle l'ellipse génératrice est un cercle.
Un sphéroïde est un cas particulier d'un ellipsoïde où 2 des 3 axes principaux sont égaux.
Volume
Sphéroïde Prolate :
- Le volume est
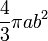
Sphéroïde Oblate :
- Le volume est
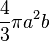
où
- a est la demi longueur de l'axe principal
- b est la demi longueur de l'axe secondaire
Aire de Surface
Un sphéroïde prolate a comme surface:
-
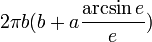
Un sphéroïde oblate a comme surface:
Ici e est l' excentricité de l'ellipse, définie comme