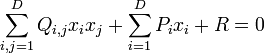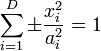Quadrique - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs est disponible ici.

En mathématiques, une quadrique, ou surface quadratique, est n'importe quelle surface de l'espace euclidien usuel de dimension 3 représentée par une équation de deuxième ordre via des variables spatiales (coordonnées)

A x 2 + B y 2 + C z 2 + 2 D y z + 2 E x z + 2 F x y + G x + H y + I z + J = 0

avec des réels A,B,C,D,E,F non tous nuls.

Via des changements de repère, chaque quadrique peut voir son équation ramenée à une des formes normalisées. Il existe 16 formes normalisées, dont des formes dites dégénérées, comme l'ensemble vide, une droite, un plan ou encore la réunion de deux plans sécants ou parallèles... Les plus intéressantes quadriques sont :

Ellipsoïde	$x^2/a^2 + y^2/b^2 + z^2/c^2 = 1 \,$
Sphéroïde ou ellipsoïde de révolution (cas particulier d'ellipsoïde)	$x^2/a^2 + y^2/a^2 + z^2/b^2 = 1 \,$
Sphère (cas particulier de sphéroïde)	$x^2/a^2 + y^2/a^2 + z^2/a^2 = 1 \,$
Paraboloïde elliptique	$x^2/a^2 + y^2/b^2 - z = 0 \,$
Paraboloïde circulaire	$x^2/a^2 + y^2/a^2 - z = 0 \,$
Paraboloïde hyperbolique	$x^2/a^2 - y^2/b^2 - z = 0 \,$
Hyperboloïde à une nappe	$x^2/a^2 + y^2/b^2 - z^2/c^2 = 1 \,$ ,
Hyperboloïde à deux nappes	$x^2/a^2 - y^2/b^2 - z^2/c^2 = -1 \,$ ,
Cône	$x^2/a^2 + y^2/b^2 - z^2/c^2 = 0 \,$ ,
Cylindre elliptique	$x^2/a^2 + y^2/b^2 = 1 \,$ ,
Cylindre circulaire	$x^2/a^2 + y^2/a^2 = 1 \,$ ,
Cylindre hyperbolique	$x^2/a^2 - y^2/b^2 = 1 \,$ ,
Cylindre parabolique	$\displaystyle{x^2 = 2 p y}$ ,

La détermination des formes normalisées se fait par l'intermédiaire de l'étude et de la réduction de la forme quadratique

Q (x, y, z) = A x 2 + B y 2 + C z 2 + 2 D y z + 2 E x z + 2 F x y

naturellement associée à l'équation.

En tant que forme quadratique, on peut associer $Q$ à la matrice symétrique suivante :

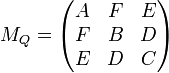
$M_Q=\begin{pmatrix} A & F & E \\ F & B & D \\ E & D & C\end{pmatrix}$

dont les valeurs propres sont toutes réelles puisque la matrice est symétrique ; ces valeurs propres permettent une classification aisée des quadriques - selon la nature des autres termes de l'équation descriptive. Dans un cas non dégénéré, au moins l'une de ses valeurs propres n'est pas identiquement nulle. Notons les $λ,μ,ν$ et supposons qu'on a déjà eu recours à une diagonalisation de l'équation afin d'obtenir la forme équivalente :

$Q (x, y, z) = λ x 2 + μ y 2 + ν z 2 + a x + b y + c z + d$

On note ici que si une des valeurs propres n'est pas nulle, on peut recentrer la coordonnée correspondante et faire ainsi disparaître le terme linéaire correspondant. En cas contraire, cela signifie que la quadrique est un paraboloïde ou un cylindre à base parabolique.

Classification en géométrie euclidienne

Classification en géométrie affine

Classification en géométrie projective

Quadrique en dimension quelconque

Plus généralement, dans un espace de dimension D, si les coordonnées de l'espace sont $\{x1, x2, \dots, xD\}$ , la quadrique générale est une hypersurface définie par l'équation algébrique :