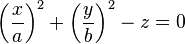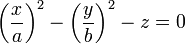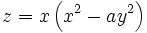Paraboloïde - Définition
En mathématiques, un paraboloïde est une surface du second degré de l'espace euclidien. Il fait donc partie des quadriques, avec pour caractéristique principale de ne pas posséder de centre de symétrie.
Certaines sections d'un paraboloïde avec un plan sont des paraboles. D'autres sont, selon le cas, des ellipses ou des hyperboles. On distingue donc les paraboloïdes elliptiques et les paraboloïdes hyperboliques.
Paraboloïde elliptique
Cette surface peut s'obtenir en faisant glisser une parabole sur une autre parabole tournant sa concavité dans la même direction.
Dans un repère bien choisi, son équation est de la forme
Le cas a = b fournit, en repère orthonormal, le cas particulier du paraboloïde de révolution. Ses sections avec un plan perpendiculaire à l'axe de rotation sont alors des cercles. Le schéma ci-contre représente, pour x et y compris entre -1 et 1, la surface d'équation z = x2 + y2. Les cercles " horizontaux " se voient en trait bleu-vert et les paraboles " verticales " en trait jaune.
Cette surface possède des applications classiques dans le domaine des miroirs. Elle donne sa forme autant à des projecteurs comme les phares de voiture qu'à des capteurs comme les antennes paraboliques ou les fours solaires tels que celui d'Odeillo près de Font-Romeu dans les Pyrénées-Orientales. L'avantage d'une surface parabolique par rapport à une découpe sphérique est la concentration des rayons réfléchis en un seul point : le point focal. Une surface sphérique ne va pas réflechir les rayons en un seul point mais va les disperser sur son axe de rotation en fonction de l'angle d'incidence.
Le volume du bol paraboloïde elliptique de hauteur h est donné par la formule
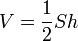
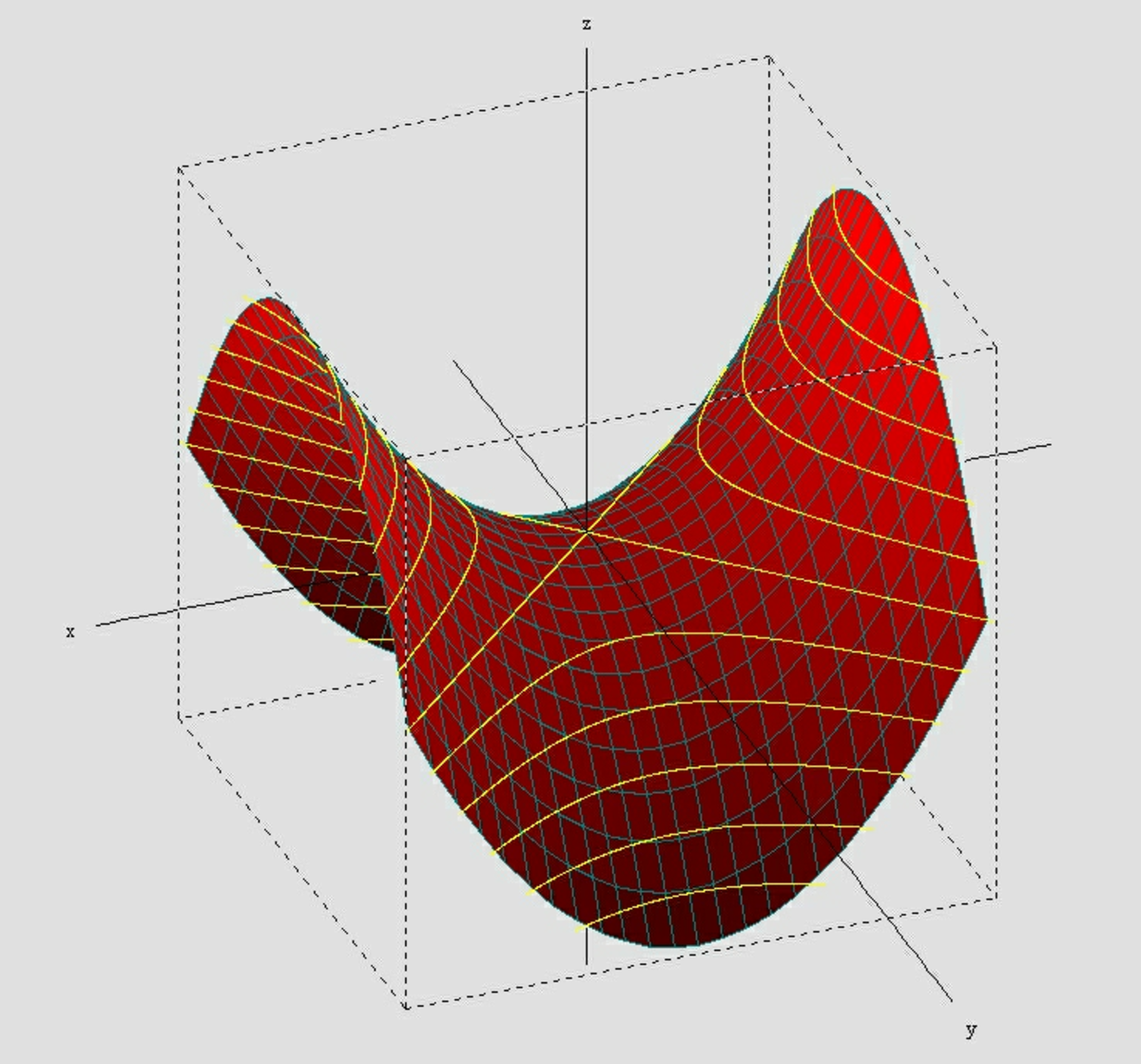
Paraboloïde hyperbolique
Cette surface peut s'obtenir en faisant glisser une parabole sur une autre parabole tournant sa concavité dans la direction opposée. C'est aussi une surface réglée qu'on peut engendrer par le déplacement d'une droite s'appuyant sur deux droites fixes non coplanaires.
Dans un repère bien choisi, son équation est de la forme
La forme particulière de cette surface lui vaut le surnom de selle de cheval. Le schéma ci-contre représente, pour x et y compris entre -1 et 1, la surface d'équation
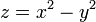
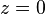
La selle de cheval se distingue de la selle de singe (lien), plus générique, parce qu'elle représente un minimax (selon le plan sécant utilisé, on trouve soit un minimum, soit un maximum). La selle de singe n'a pas cette propriété. Elle peut être visualisée comme une selle sur laquelle un singe pourrait s'asseoir sans gêner ses jambes ni sa queue. Voici un exemple de selle de singe :
| Les solides géométriques | ||||
| Les solides de Platon | ||||
| Tétraèdre - Cube - Octaèdre - Icosaèdre - Dodécaèdre | ||||
| Les solides d'Archimède | ||||
| Tétraèdre tronqué - Cube tronqué - Octaèdre tronqué - Dodécaèdre tronqué - Icosaèdre tronqué - Cuboctaèdre - Cube adouci - Icosidodécaèdre - Dodécaèdre adouci - Petit rhombicuboctaèdre - Grand rhombicuboctaèdre - Petit rhombicosidodécaèdre - Grand rhombicosidodécaèdre | ||||
| Les solides de Kepler-Poinsot | ||||
| Petit dodécaèdre étoilé - Grand dodécaèdre étoilé - Grand dodécaèdre - Grand icosaèdre | ||||
| Les solides de Catalan | ||||
| Triakioctaèdre - Tétrakihexaèdre - Triakitétraèdre - Pentakidodécaèdre - Triaki-icosaèdre - Dodécaèdre rhombique - Icositétraèdre pentagonal - Triacontaèdre rhombique - Hexacontaèdre pentagonal - Icositétraèdre trapézoïdal - Hexakioctaèdre - Hexacontaèdre trapézoïdal - Hexaki icosaèdre | ||||
| Les solides de Johnson | ||||
| Les solides de révolution | ||||
| Sphère - Cylindre de révolution - Cône de révolution - Tore - Paraboloïde de révolution |