Spline - Définition
Dans le domaine mathématique de l'analyse numérique, une spline est une fonction définie par morceaux par des polynômes.
Dans les problèmes d'interpolation, la méthode des splines est souvent préférée à l'interpolation polynomiale, car on obtient des résultats similaires en se servant de polynômes ayant des degrés inférieurs, tout en évitant le phénomène de Runge.
Dans le domaine du design, en construction automobile par exemple, les splines sont utilisées pour approcher des contours complexes. Leur simplicité d'implémentation les rend très populaires et elles sont fréquemment utilisées dans les logiciels de dessin.
Définition
Étant donnés k points ti appelés nœuds dans un intervalle [a,b] avec
La courbe S
est appelée spline de degré n si
et sa restriction sur chaque sous-intervalle
-
![S_{[t_i,t_{i+1}]} \in P_n \mbox{ , } i = 0,\ldots k-2](https://static.techno-science.net/illustration/Definitions/autres/7/783f73e4782aa0e4694a70df39b77c0b_8853fc801a2b56baf5eb538aa3dbd92a.png)
En d'autres termes, sur chaque sous-intervalle
S est un polynôme de degré n.
Les (ti, S(ti)) sont appelés points de contrôle.
Exemple
La fonction spline la plus simple est de degré 1, ce qui correspond à un polygone.
La plus couramment utilisée est la spline de degré 3 qui vérifie la propriété suivante :
S''(a) = S''(b) = 0
En dehors de l'intervalle, la courbe est une ligne droite tout en conservant le lissage.
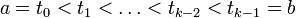
![S:[a,b] \to \mathbb{R}](https://static.techno-science.net/illustration/Definitions/autres/6/657900f76cf7e30d7258beca0a49f9ad_729d3b2444429a3ee8f8be2f3764be1e.png)
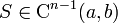
![[t_i,t_{i+1}] \mbox{ , } i = 0,\ldots k-2](https://static.techno-science.net/illustration/Definitions/autres/c/c96da3e467f710575dfa0de3a1789f66_3cae5f0663a2ff10825c850618c088a1.png)

















































