Spirale - Définition
(voir page de discussion)
Spirale n.f. ( du lat. Spira ; du gr. Speira: enroulement.) Définition générale et encyclopédique Article paru dans le "Larousse du XXème siècle" édition 1930
Géom. Courbe qui fait sur un plan plusieurs révolutions autour d'un point dont elle s'écarte de plus en plus : il y a une infinité de sortes de spirales, parmi lesquelles celle d'Archimède est la plus célèbre.
Loc. Adv. En spirale = en forme de spirale : escalier en spirale.
Pyrotechn. Nom impropre d'une pièce d'artifice disposée non en spirale mais en hélice conique.
Phys. Spirale d'Airy : phénomène de polarisation rotatoire qui se produit lorsqu'on observe, entre deux tournalines croisées, deux lames de quartz de même épaisseur mais de rotation inverse.
Encycl.Géom. On nomme généralement spirale une courbe dont le rayon polaire croît suivant une loi d'ailleurs quelconque, en même temps qu'il tourne toujours dans le même sens autour du pôle. Une spirale a nécessairement une infinité de spires distinctes; le rayon polaire peut croître indéfiniment avec l'angle, ou tendre vers une limite finie; dans ce dernier cas, la spirale est asymptote à un cercle et même parfois à une droite (spirale hyperbolique). Le rayon polaire diminue lorsqu'on lui donne un mouvement contraire, et il peut tendre soit vers zéro, soit vers une limite quelconque; dans le premier cas, la spirale a pour asymptote le pôle lui-même; dans le second, elle a pour asymptote un cercle. Les spirales les plus connues sont : la spirale d'Archimède représentée en coordonnées polaires par l'équation : ρ=ρo + rΘ, le rayon vecteur issu du pôle est proportionnel à l'angle polaire correspondant; la spirale hyperbolique : ρ=a/Θ, le rayon est inversement proportionnel à l'angle polaire; et la spirale logarithmique : ρ=abθ, qui coupe sous un même angle tous les rayons vecteurs.
Dess.graph.
L'éloignement progressif d'une spirale dépend du nombre des centres qui ont servi à la former. Il y a des spirales :
- à 2 centres qui sont situés sur une même ligne,
- à 3 centres qui sont situés aux trois sommets d'un triangle équilatéral,
- à 4 centres qui sont situés aux quatre sommets des angles d'un carré.
- etc.
Pour décrire d'un mouvement continu des spirales suffisamment régulières quand il s'agit, par exemple de la décoration des jardins, voici le procédé: Attachez un cordeau à un piquet fiché verticalement en terre à l'endroit où doit se trouver le centre de la spirale. Enroulez ensuite le cordeau autour du piquet et attachez une pointe à l'extrémité mobile du cordeau : déroulez celui-ci en le tenant tendu, en ayant soin de bien appuyer la pointe verticalement sur le terrain de manière à tracer la courbe à mesure que le cordeau se déroule. Dans ce procédé, les spires de la ligne tracée sont évidemment d'autant plus écartées, que le piquet central est plus gros.
Bot. Les feuilles sont insérées sur la tige en des points qui sont situés sur une spirale (l'angle dièdre passant par l'axe de la tige et deux points qui se succèdent est la divergence, valeur caractéristiques de l'espèce).
En mathématiques, une spirale est une courbe plane qui tourne autour d'un point ou d'un axe central en s'en éloignant ou s'en rapprochant de plus en plus selon la manière dont vous suivez la courbe.
Spirale à deux dimensions
Une spirale à deux dimensions peut être décrite à l'aide de coordonnées polaires. C’est-à-dire qu'on peut exprimer r (le rayon) comme étant un fonction continue et monotone de θ (l'angle).
Il existe plusieurs types de spirales à deux dimensions. Voici les plus importantes :
- La spirale d'Archimède :
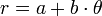
- La spirale hyperbolique :
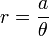
- La spirale logarithmique :
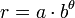
- La spirale de Fermat :
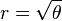
- La spirale de Nielsen
- La spirale de Cotes
- La spirale de Galilée
- La spirale de Fibonacci
Construction d'une spirale approximative
Se munir d'une feuille de papier, d'un compas et d'une règle.
- 1. Tracer une droite qui partage la feuille en deux parties égales.
- 2. Placer deux points A1 et A2 sur la droite aux environs du centre de la feuille. La distance entre le point A1 et le point A2 paramètre la concentration de la courbe. Plus cette distance est courte, plus la spirale sera concentrée.
- 3. Piquer le compas sur le point A1. L'écarter de la distance A1A2.
- 4. Tracer le demi-cercle d'origine A2. Noter A3 le point issu de l'intersection entre le demi-cercle et notre droite.
- 5. Piquer le compas sur le point A2. L'écarter de la distance A2A3.
- 6. Tracer le demi-cercle d'origine A3. Noter A4 le point issu de l'intersection entre le demi-cercle et notre droite.
- 7. Piquer le compas sur le point A3. L'écarter de la distance A3A4.
- 8. Tracer le demi-cercle d'origine A4. Noter A5 le point issu de l'intersection entre le demi-cercle et notre droite.
- 9. etc.
Le résultat est une spirale construite à partir de demi-cercles dont le rayon double à chaque fois.
On peut imaginer plusieurs variantes combinables :
- le rayon de chaque demi-cercle ne double pas mais est plutôt augmenté d'une valeur fixe.
- tracer des quarts de cercles au lieu de demi-cercles (nécessite deux droites perpendiculaires)
Culture populaire
- Le film japonais Uzumaki.
- Le film américain Pi.


















































