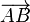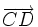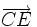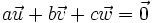Coplanaire - Définition
Étymologiquement, plusieurs objets sont coplanaires si et seulement s'ils sont situés dans un même plan. En géométrie, on distinguera les points coplanaires et les vecteurs coplanaires.
Points coplanaires
Des points coplanaires sont des points situés dans un même plan. Deux points ou trois points sont toujours coplanaires. En effet, deux points sont toujours sur une même droite qui peut être plongée dans un plan. De même, trois points, ou bien sont alignés et la droite peut être plongée dans un plan, ou bien définissent un plan.
La notion de points coplanaires ne devient donc intéressante que si l'on considère au moins quatre points. C'est la raison pour laquelle un tabouret à trois pieds n'est jamais bancal, même si son assise peut ne pas être horizontale, alors qu'une table à quatre pieds peut être bancale et nécessiter une cale qui placera l'un des pieds dans le même plan que les trois autres.
Vecteurs coplanaires
Trois vecteurs sont coplanaires si et seulement si on peut trouver trois représentants de ces vecteurs situées dans un même plan.
Attention, le fait qu'initialement les premiers représentants choisis ne soient pas dans un même plan n'empêche absoluement pas les vecteurs d'être coplanaires. Cela signifie seulement que l'on n'a pas choisi les "bons" représentants.
Par exemple, dans un cube, ABCDEFGH, les points ABCGH ne sont pas coplanaires mais les vecteurs
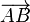
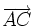
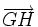
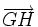
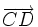
En revanche, s'il a suffi de 4 points pour écrire des représentants des trois vecteurs, les trois vecteurs sont coplanaires si et seulement si les quatre points sont coplanaires.
En géométrie analytique, les vecteurs
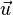
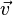
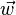
Ainsi, les trois vecteurs forment une famille liée.
La notion de vecteurs coplanaires est importante pour prouver
- l'appartenance d'un point à un plan : le point D appartient au plan ABC si et seulement si les vecteurs
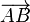
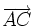
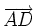
- le parallélisme d'une droite et d'un plan : la droite (AB) est parallèle au plan (CDE) si et seulement si les vecteurs