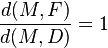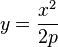Parabole - Définition

La parabole est l'intersection d'un plan avec un cône lorsque le plan est parallèle à l'une des génératrices du cône. Elle est un type de courbe dont les nombreuses propriétés géométriques ont intéressé les mathématiciens dès l'Antiquité et ont reçu des applications techniques variées.

Mathématiques

Section conique

Les paraboles font partie de la famille des coniques, c'est-à-dire des courbes qui s'obtiennent par l'intersection d'un cône de révolution avec un plan ; en l'occurrence, la parabole est obtenue lorsque le plan est parallèle à l'une des génératrices du cône.

Directrice, foyer et excentricité

Soient D une droite et F un point n'appartenant pas à D, et soit P le plan contenant la droite D et le point F). On appelle parabole de droite directrice D et de foyer F l'ensemble des points M du plan P vérifiant :

où d(M,F) mesure la distance du point M au point F et d(M,D) mesure la distance du point M à la droite D. C'est donc une conique dont l'excentricité e vaut 1

Équations

À partir du foyer et de la directrice

Si la parabole est donnée par son foyer F et sa directrice , on appelle O le projeté orthogonal de F sur , on appelle p (paramètre de la parabole) la distance OF et on appelle S le milieu de [FO]. Alors, dans le repère orthonormé où a même direction et sens que , l'équation de la parabole est :

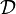
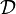
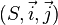
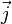
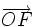
À partir de la fonction du second degré

La courbe représentative d'une fonction polynôme du second degré d'équation

y = ax² + bx + c

où a, b et c sont des constantes réelles (a non nul) est une parabole. Dans le cas a = 1, b = 0, et c = 0 on obtient une expression simple pour une parabole: y = x².

Le sommet S d'une parabole est le point de coordonnées . Son axe de symétrie est l'axe . Dans le repère , son équation est

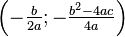
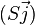
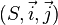
Y = aX²

Son foyer est le point et sa directrice est la droite d'équation

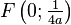
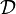
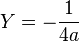
À partir de l'équation générale

Soit l'équation Ax² + 2Bxy + Cy² + 2Dx + 2Ey + F = 0, dans un repère orthonormal. Si B² − AC = 0 alors cette équation est celle d'une parabole ou de deux droites parallèles.

Soit l'équation Ax² + Cy² + 2Dx + 2Ey + F = 0, dans un repère orthonormal. Si AC = 0 avec AE ou DC non nul alors cette équation est celle d'une parabole.

Enfin, dans tout repère orthonormal, l'équation d'une parabole est de la forme

Ax² + 2Bxy + Cy² + 2Dx + 2Ey + F = 0 avec B² − AC = 0.

Paramétrisation

Dans le repère où O est le point situé au milieu du segment constitué du foyer F et de sa projection H sur la directrice et où est un vecteur unitaire orienté de O vers F, on peut envisager plusieurs paramétrisations de la parabole :

1. Une paramétrisation cartésienne par l'ordonnée : .
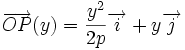
2. La paramétrisation : , pour tout

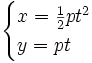
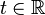
Cette paramétrisation est régulière (i.e. le vecteur dérivé ne s'annule pas). Le vecteur (t,1) dirige alors la tangente au point de paramètre t.

Quelques propriétés géométriques de la parabole

Cordes parallèles

Toutes les cordes parallèles ont leur milieu situé sur une droite perpendiculaire à la directrice. La tangente parallèle à cette direction a son point de contact sur cette droite. Les deux tangentes à la parabole aux extrémités d'une telle corde se coupent sur cette droite.

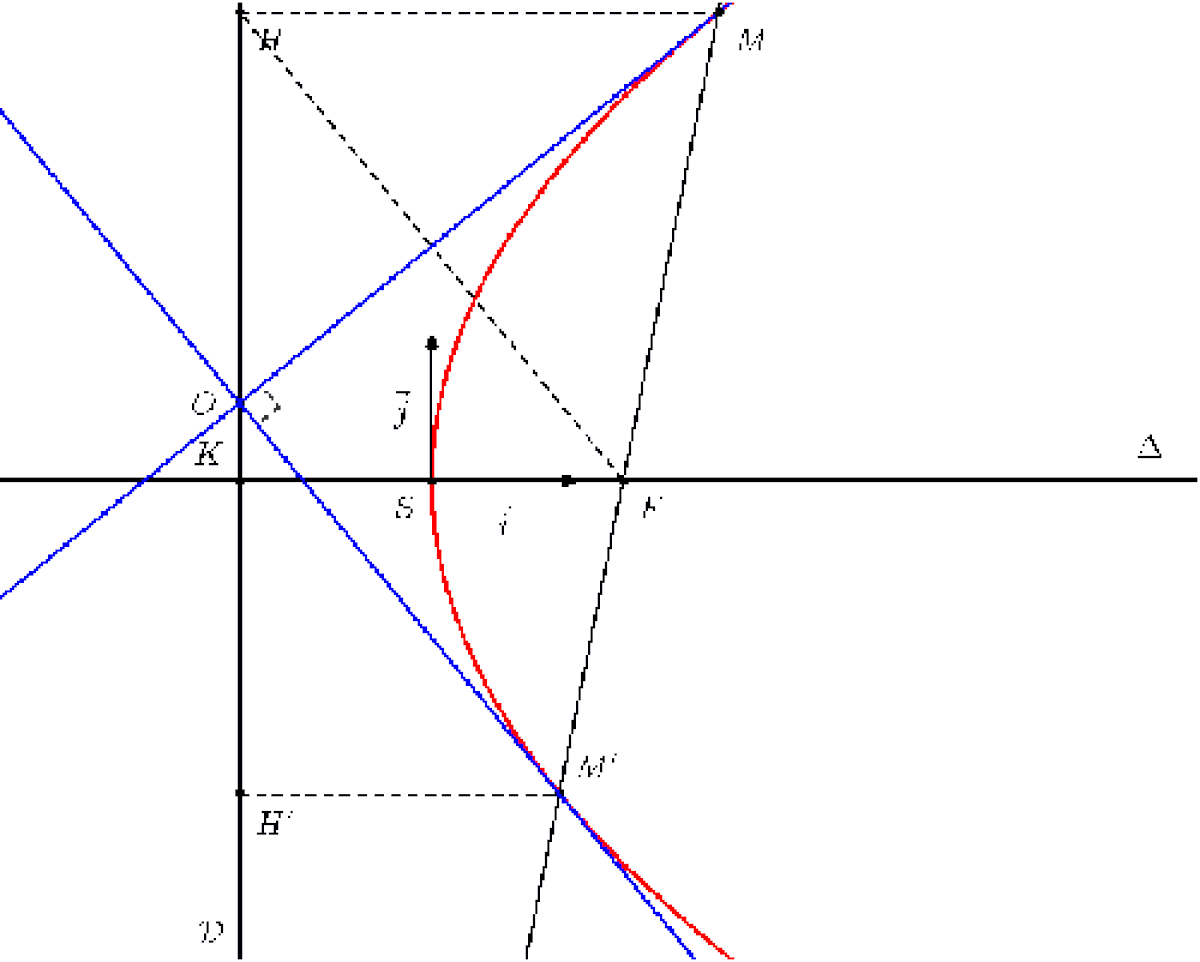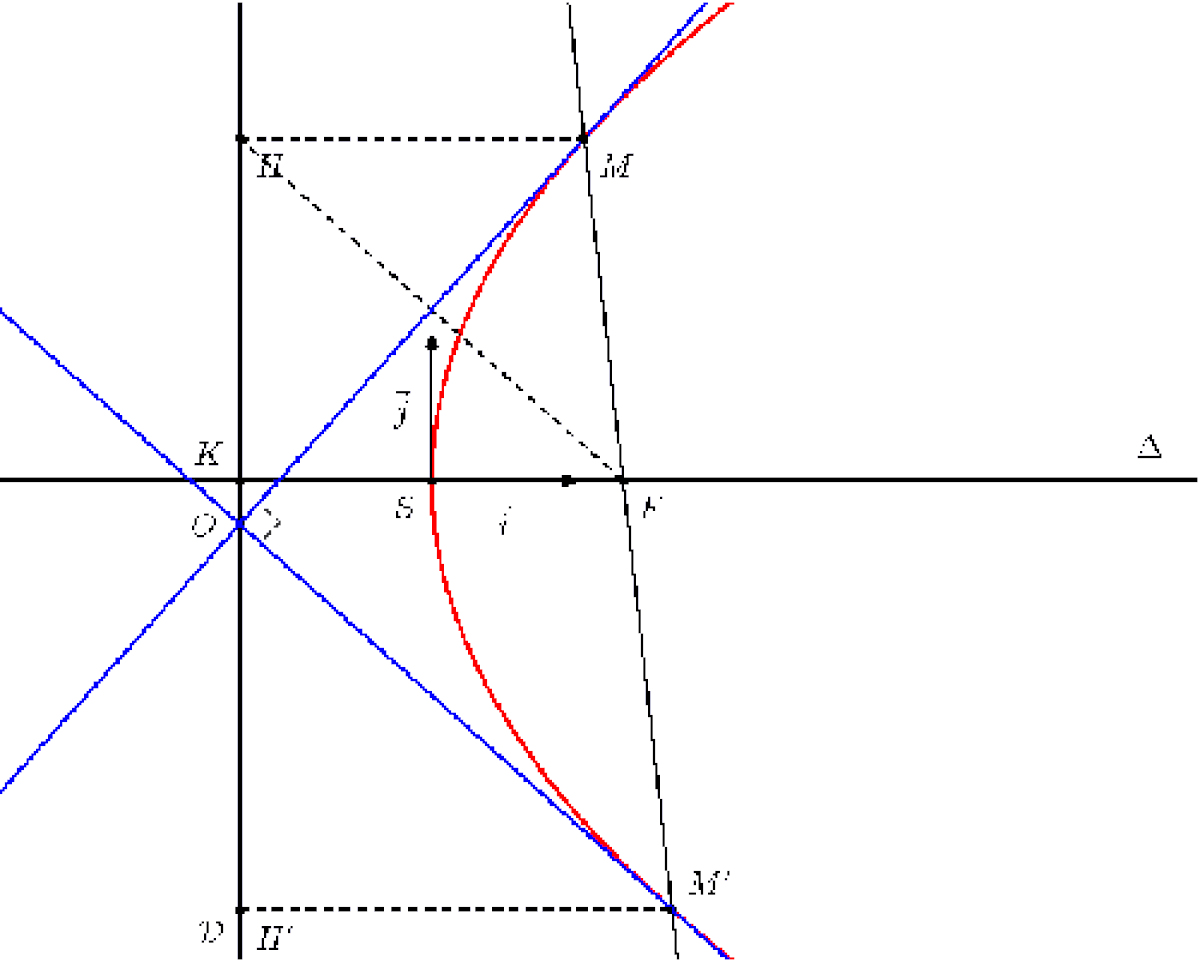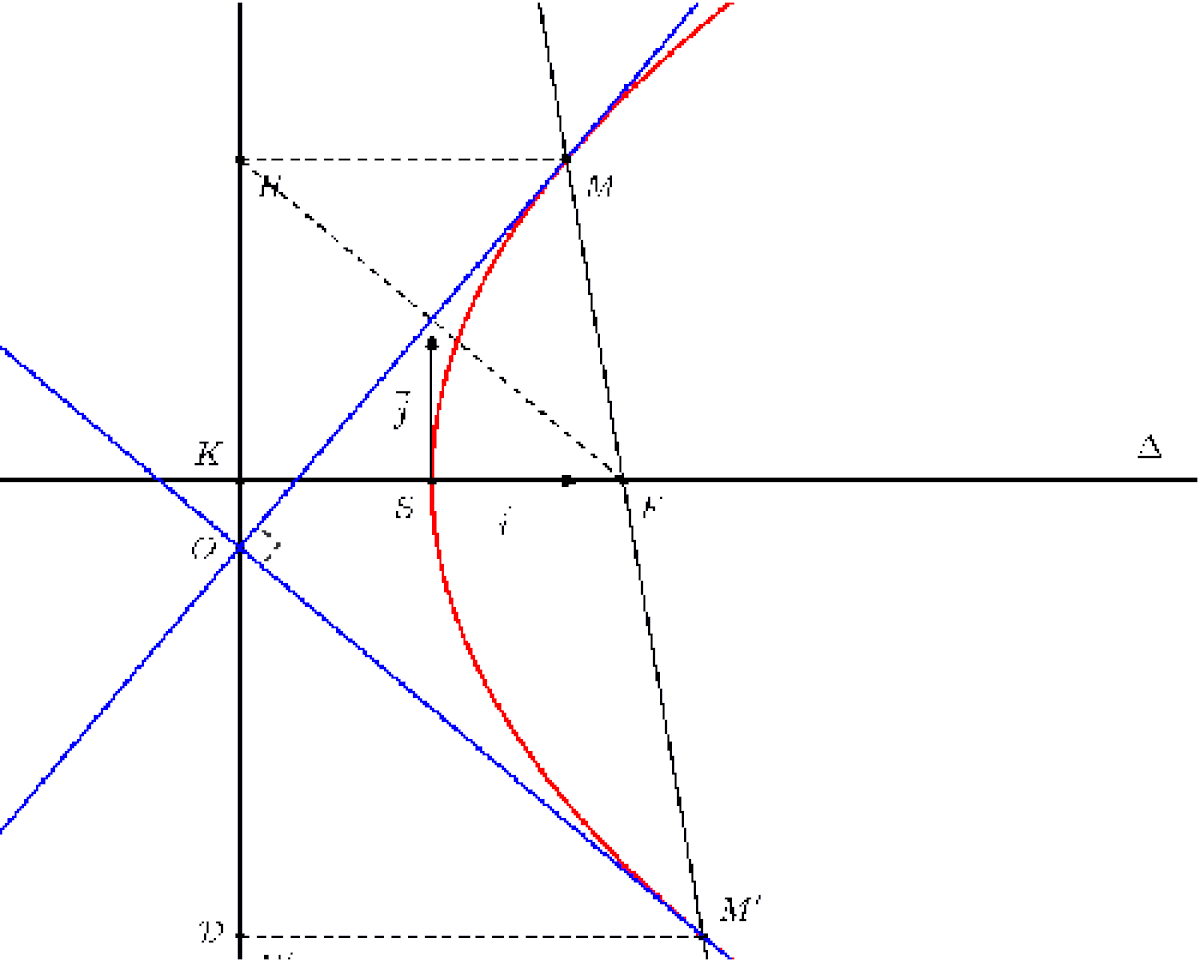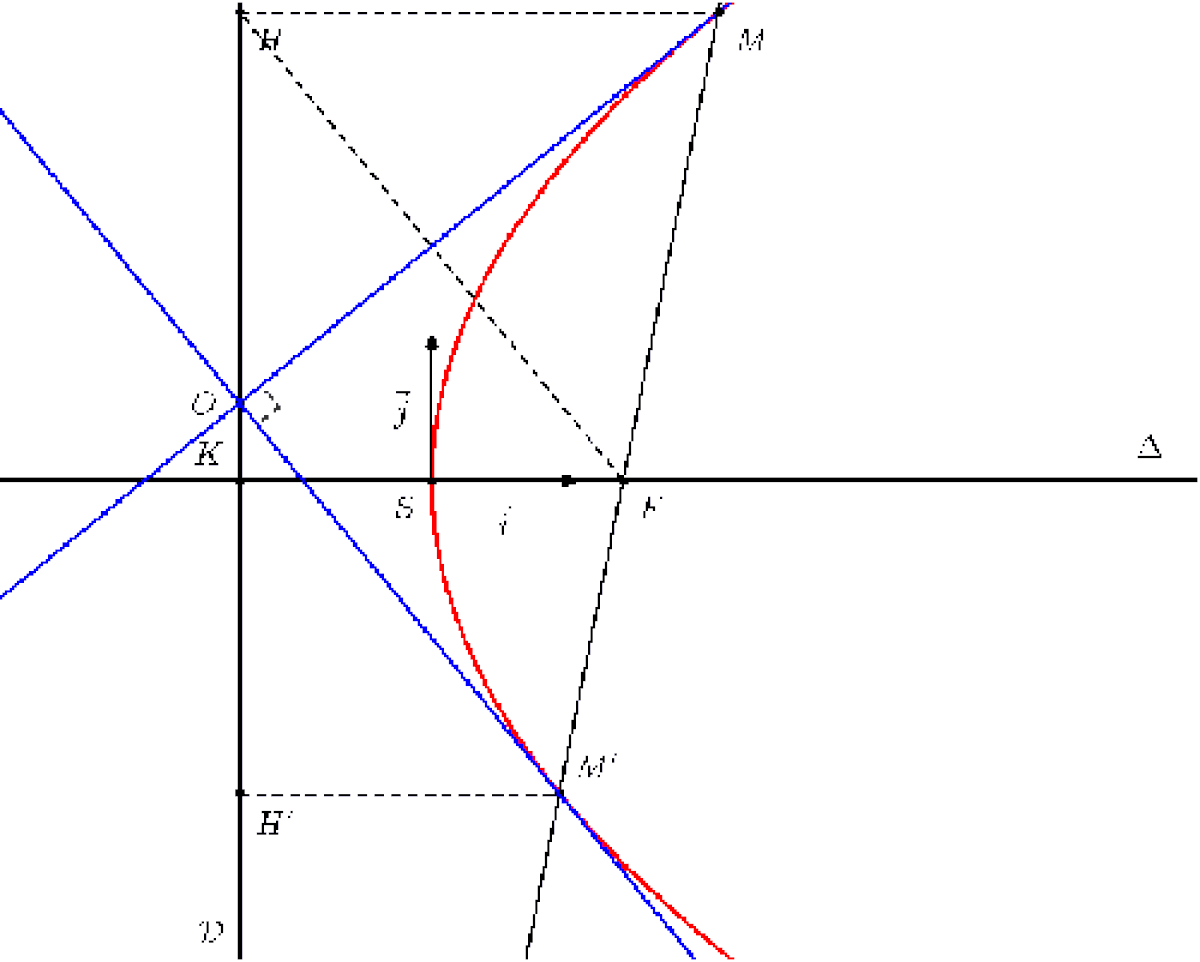
Propriété relative à l'orthoptique

En se dépaçant le long de sa directrice, la parabole est toujours vue sous un angle droit.

Soient M et M' les points d'intersection d'une droite quelconque passant par le foyer de la parabole avec la parabole. Les deux tangentes de la parabole passant par M et M' se coupent sur la directrice en formant un angle droit entre elles. De plus, en appelant H et H' les projetés respectifs de M et M' sur la directrice et O le point d'intersection des deux tangentes et de la directrice, on a que O et le milieu de [HH'].

En se déplaçant le long de sa directrice, la parabole est toujours vue sous un angle droit.

Applications

On utilise les parabole pour concentrer des ondes, ou des rayons en un point, le foyer de la parabole. Les paraboles sont également utilisées pour concentrer les rayons solaires en un point. Par exemple, on peut faire passer de l'eau dans un tuyau qui passe par le foyer d'un concentrateur solaire, cette eau monte alors très vite en température, voire même se vaporise. Qui dit vaporisation, dit augmentation de pression. On peut ensuite utiliser cette pression pour faire tourner un alternateur pour produire de l'électricité.

Physique

trajectoire parabolique

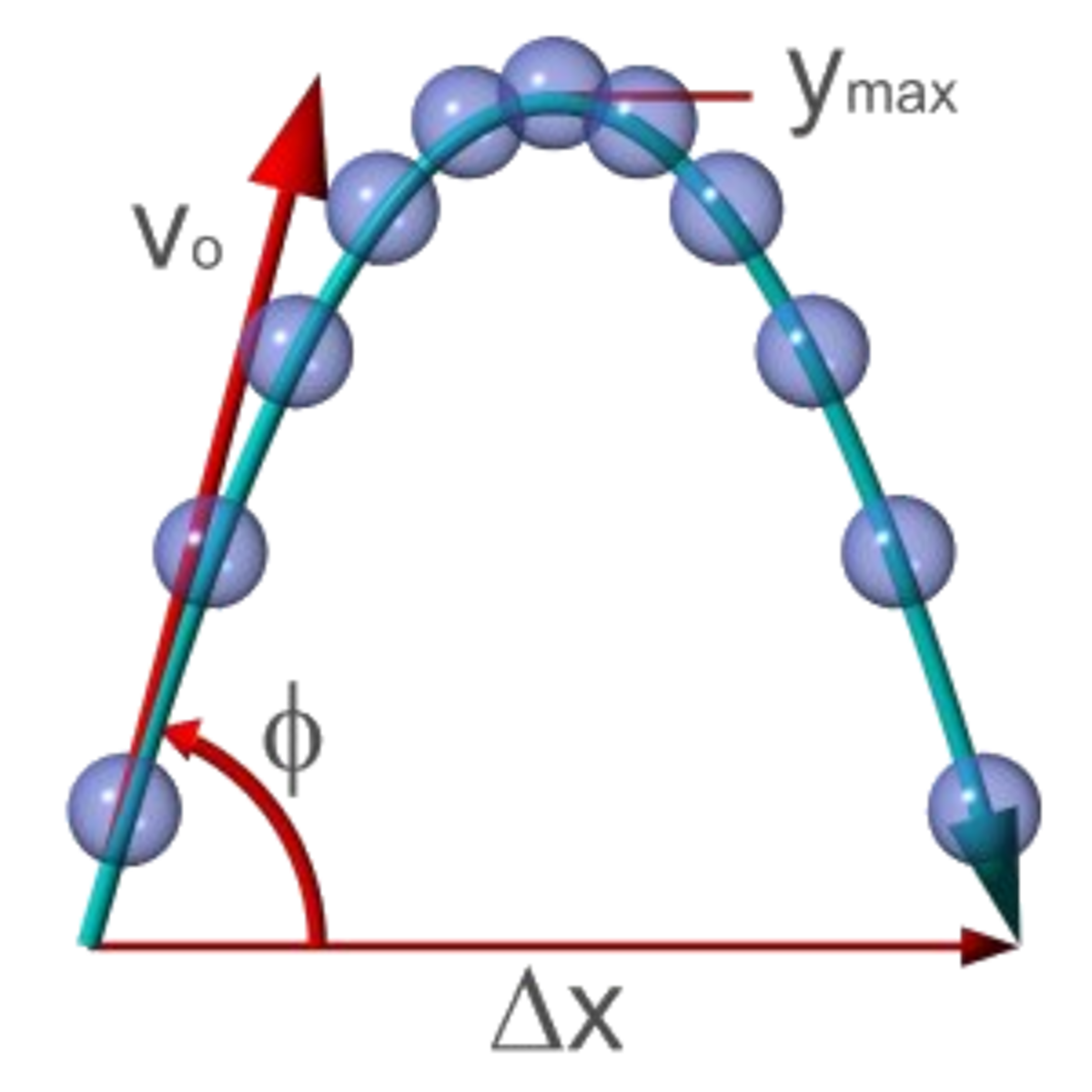
La parabole est la trajectoire décrite par un objet que l'on lance si on peut négliger la courbure de la Terre, le frottement de l'air (vent, ralentissement de l'objet) et la variation de la gravité avec la hauteur.

A noter également que l'énergie mécanique pour un objet décrivant une parabole est toujours nulle.

Ondes hertziennes

Par métonymie, une parabole désigne une antenne parabolique. Il s'agit plus exactement d'une application des propriétés de la surface nommée paraboloïde de révolution.