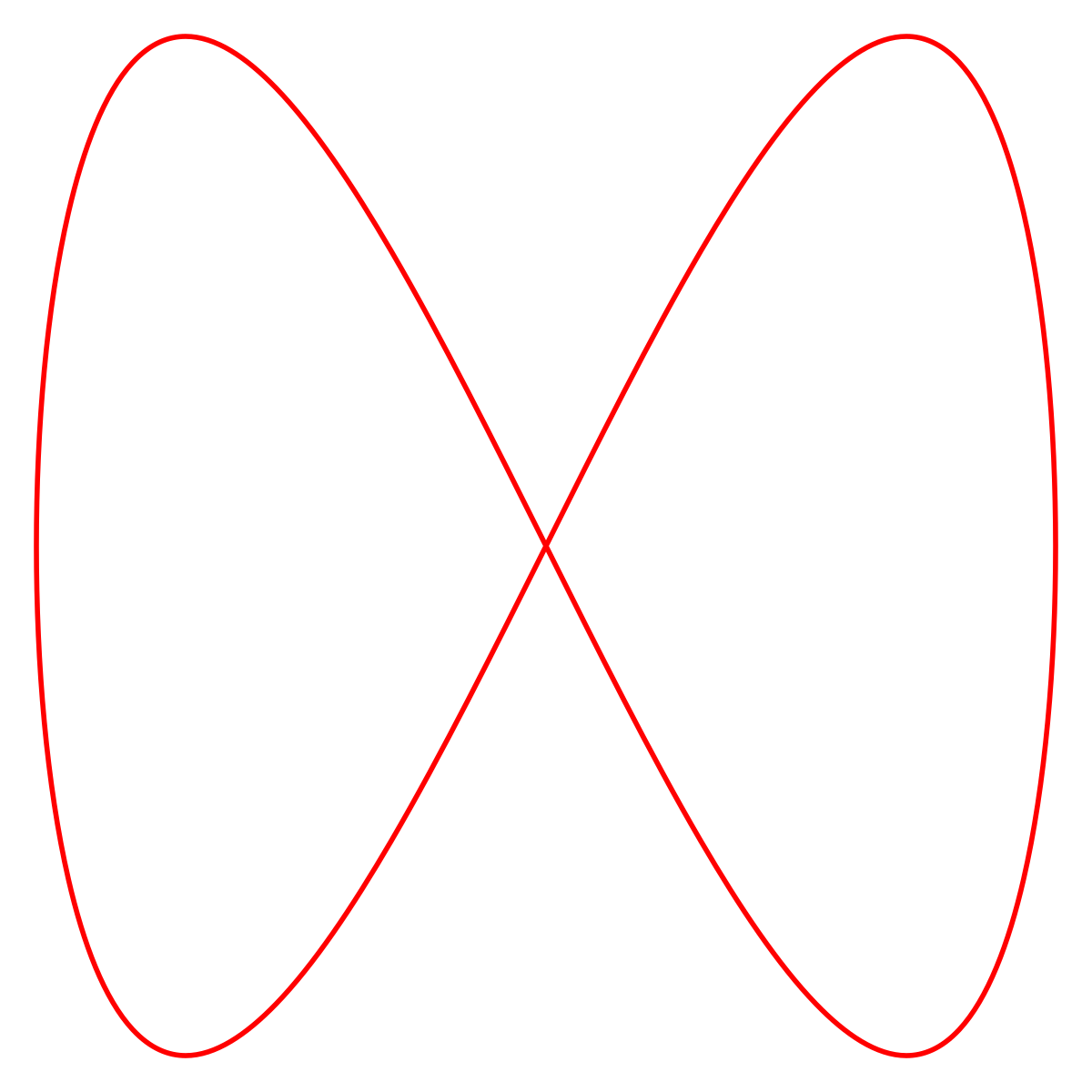
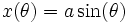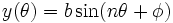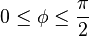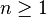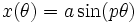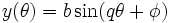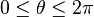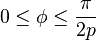Courbe de Lissajous - Définition
La courbe de Lissajous, aussi dénommée figure de Lissajous ou courbe de Bowditch, est la trajectoire d'un point dont les composantes rectangulaires ont un mouvement sinusoïdal.
Cette famille de courbes fut étudiée par Nathaniel Bowditch en 1815, puis plus en détail par Jules Lissajous en 1857.
Définition mathématique

Courbe de Lissajous obtenue sur un oscilloscope
Une courbe de Lissajous peut être définie par l'équation paramétrique suivante :
|
|
où
|
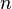
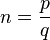
|
|
où
|
Propriétés
- Si n est irrationnel, la courbe est dense dans le rectangle [-a,a]x[-b,b].
- Si n est rationnel,
- la courbe est une courbe algébrique de degré 2q si
![\phi \in \left]0,\frac{\pi}{2p} \right]](https://static.techno-science.net/illustration/Definitions/autres/7/73d3423f751211c592c2686ae217f1e4_dbc578335bd7c06b4cda80f36d6f74bd.png)
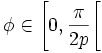
- la courbe est une portion de courbe algébrique de degré q si
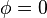
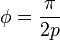
- la courbe est une courbe algébrique de degré 2q si
- Si n est un entier pair et
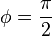
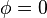
Cas particuliers
- si a=b et n=1, la courbe est une ellipse.
- si
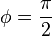
- si
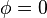
- si
- si a=b et n=q=2 (donc p=1), la courbe est une besace
- si
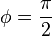
- si
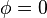
- si
Voici quelques exemples de tracés avec φ = 0, p impair, q pair, |p − q| = 1.