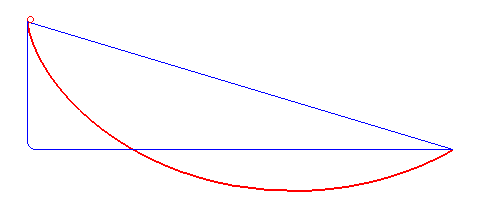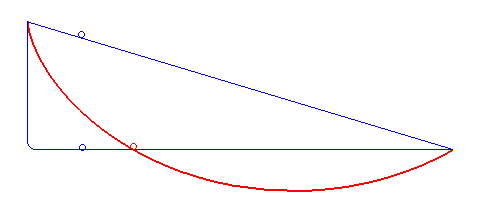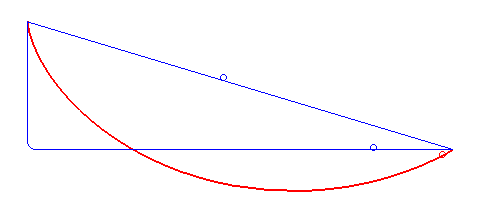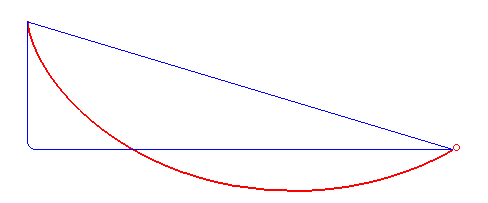
Courbe brachistochrone - Définition
Le mot brachistochrone désigne une courbe plane sur laquelle un point matériel pesant placé dans un champ de pesanteur uniforme, glissant sans frottement et sans vitesse initiale, présente un temps de parcours minimal parmi toutes les courbes joignant deux points fixés : on parle de problème de la courbe brachistochrone.
Étymologie
Le mot brachistochrone vient du grec brakhisto (" le plus court ") et s'écrit donc avec un i et non un y, et de chronos (" temps "). Elle fut étudiée et nommée ainsi par Jean Bernoulli.
Histoire
La résolution du problème de la courbe brachistochrone passionna les mathématiciens. Isaac Newton fut mis au défi de le résoudre en 1696 et y serait parvenu en seulement une journée. En fait, la solution fut découverte en même temps par Leibniz, Newton, L'Hôpital, Jean et Jacques Bernoulli : il s'agit d'un arc de cycloïde commençant avec une tangente verticale.
Les méthodes imaginées pour sa résolution amenèrent à développer la branche des mathématiques qu'on appelle le calcul des variations.
Démonstration de la solution
Démonstration historique (par Bernouilli)
Le chemin le plus court entre deux points est celui que suivrait un rayon de lumière. La courbe brachistochrone est donc simplement le trajet suivi par la lumière dans un milieu où la vitesse augmente selon une accélération constante (l’attraction terrestre g). La loi de la conservation de l’énergie permet d’exprimer la vitesse d’un corps soumis à l’attraction terrestre par:
,
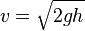
où h représente la perte d’altitude par rapport au point de départ. Il est à noter que la vitesse ne dépend pas du départ horizontal.
La loi de la réfraction indique que tout au long de sa trajectoire un rayon lumineux obéit à la règle
,
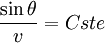
où θ représente l’angle par rapport à la verticale. En insérant dans cette formule l’expression de la vitesse trouvée plus haut, on constate immédiatement deux choses:
1- Au point de départ, lorsque la vitesse est nulle, l’angle doit nécessairement être nul. Donc la courbe brachistochrone est tangente à la verticale à l’origine.
2- La vitesse est bornée car le sinus ne peut être supérieur à 1. Cette vitesse maximum est atteinte quand la particule (ou le rayon) passe par l’horizontale (ce " passage " pouvant être asymptotique.)
Sans restreindre la généralité du problème, on va supposer que la particule part du point de coordonnées (0,0) et que la vitesse maximum est atteinte à l’altitude –D. La loi de la réfraction s’exprime alors par:
.
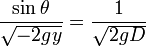
Sachant que la particule se déplace sur une courbe, on a la relation :
.
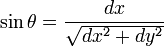
En insérant cette expression dans la formule précédente et en réarrangeant les termes on trouve:
.
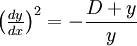
Ce qui est l’équation différentielle de l’opposée d’une cycloïde, générée par un cercle de diamètre D.
Démonstration avec le Calcul des variations
On note C(t) = (x(t),y(t)) la courbe recherchée, paramétrée par t. L'équation cartésienne est y = f(x) (on exclut les courbes ayant des parties verticales). On exprime un déplacement infinitesimal sur la courbe:
. Si on pose que la dérivée de la courbe est 
, on a: 
.
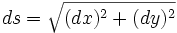
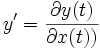
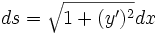
Mais, d'autre part, on a toujours, en vertu du théorème de l'énergie cinétique, la relation suivante:
.
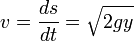
On peut alors exprimer le temps de parcours infinitésimal dt:
. Donc 
. Avec T le temps de parcours (à minimiser), xa et xb les abscisses de départ et d'arrivée.
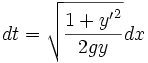
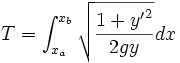
Il s'agit donc de trouver le minimum de la fonctionnelle 
. Les points critiques d'une telle fonctionnelle sont donnés par l'équation d'Euler-Lagrange. Après calcul et simplification, on obtient que y est un point critique de F si :
.
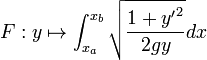
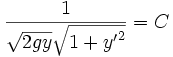
On obtient donc l'équation différentielle ![\left[ 1 + {y'}^2 \right] y = k^2](https://static.techno-science.net/illustration/Definitions/autres/3/3555dafcf13f680f617e13052b31e2d0_4d4cdaaf5dc67d2d825d40ab3d916ed5.png){kind=small}
Résolution de l'équation différentielle et solution
Pour résoudre , on procède au changement de variable suivant:
. Dans ce cas, on obtient l'équation paramétrique de la courbe solution:
,
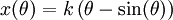
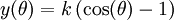
Il s'agit de la cycloïde sous sa forme paramétrée: