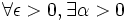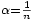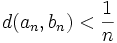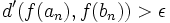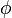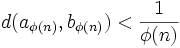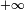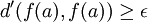Théorème de Heine - Définition
Le théorème de Heine, nommé ainsi en l'honneur de Édouard Heine, s'énonce ainsi : Soit deux espaces métriques X et Y, tel que X soit également compact. Alors toute application continue de X dans Y est uniformément continue. Cela implique notamment que toute fonction continue de I = [a,b] dans

Enoncé et démonstration pour les fonctions numériques
Enoncé
Soient (a,b) dans R² avec a
On dit alors que f est uniformément continue sur [a,b] Soit ε > 0 fixé et
Si Q est un point du segment [a,b] alors il lui correspond un α(Q) tel que pour tout point P de [a,b]
Soit I(Q) l'intervalle de milieu Q et de longueur α(Q). Ces I(Q) recouvrent [a,b], mais d'après le Théorème de Borel-Lebesgue il suffit d'un recouvrement fini d'entre eux pour recouvrir [a,b] soit α la longueur du plus petit de ces intervalles en nombre fini Soient P et P' deux points de [a,b] tel que
P appartient à un intervalle I(Q') et
Or
Comme (1) implique (2) on obtient
On se place dans le cas général de deux espaces métriques X et Y avec X compact. On note d la distance sur X et d' la distance sur Y. Le théorème de Heine nous dit alors toute application continue de X dans Y est uniformément continue, ce qui s'exprime par :
Pour montrer cela, on raisonne par l'absurde en considérant f continue sur X mais non uniforménent continue. Alors, on sait qu'il existe ε > 0 tel que pour chaque
La suite (an) est à valeurs dans le compact X donc on peut en extraire une sous-suite convergente. On note
Il s'en suit, en faisant tendre n vers
On obtient là une contradiction. Donc f est uniforménent continue sur X.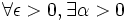
![\forall (x,x') \in [a,b]^2 |x-x'|<\alpha \Rightarrow |f(x)-f(x')|<\epsilon](https://static.techno-science.net/illustration/Definitions/autres/8/820d19cc004a734e5d932c6a6a05d4dd_35665ef966c4002769cf306737371700.png)
Démonstration
![x \in [a,b]](https://static.techno-science.net/illustration/Definitions/autres/8/8290bddba5acf9822dcbf61f4ac67d1b_92fce6cd0dff07f919fd3d074608a860.png)
Comme f est continue sur [a,b], il existe un α(x) tel que
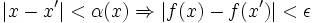
![inf (\{\alpha (x) ; x\in [a,b]\}) \geq 0](https://static.techno-science.net/illustration/Definitions/autres/e/eabe50656c3d591c353cad274e3f5887_6aab177ba6675453ac0bb4ac3c74d8e1.png)
![inf (\{\alpha (x) ; x\in [a,b]\}) \neq 0](https://static.techno-science.net/illustration/Definitions/autres/f/f9a368f760620b763d466dbec1b0aeff_230e7566f027f50a6cc63239e2e62dce.png)
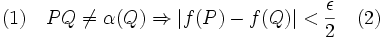
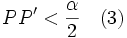
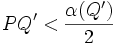
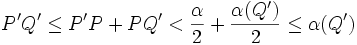
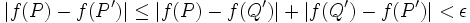
Démonstration dans le cas général en utilisant la propriété de Bolzano-Weierstrass