Sphère de Riemann - Définition
Introduction
En mathématiques, la sphère de Riemann est une manière de prolonger le plan des nombres complexes avec un point additionnel à l'infini, de manière à ce que certaines expressions mathématiques deviennent convergentes et élégantes, du moins dans certains contextes. Elle est baptisé du nom du mathématicien du 19eme siècle Bernhard Riemann. Ce plan s'appelle également la droite projective complexe, dénotée
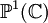
D'un point de vue purement algébrique, les nombres complexes avec un élément supplémentaire à l'infini constituent un ensemble de nombres connu sous le nom de nombres complexes prolongés. L'arithmétique de cet ensemble n'obéit pas à toutes les règles habituelles de l'algèbre; notamment les nombres complexes prolongés ne forment pas un corps. En revanche, la sphère de Riemann a un comportement géométriquement et analytiquement non divergent, même au voisinage de l'infini; c'est une variété complexe unidimensionnelle, également appelée une surface de Riemann.
En analyse complexe, la sphère de Riemann permet une expression élégante de la théorie fonctions méromorphes. La sphère de Riemann est omniprésente en géométrie projective et en géométrie algébrique comme exemple fondamental d'une variété complexe, d'un espace projectif, et d'une variété algébrique. Elle a également une utilité dans d'autres disciplines qui dépendent de l'analyse et de la géométrie, telle que la physique quantique (représentation des états quantiques) et d'autres branches de la physique (théorie des twisteurs par exemple).
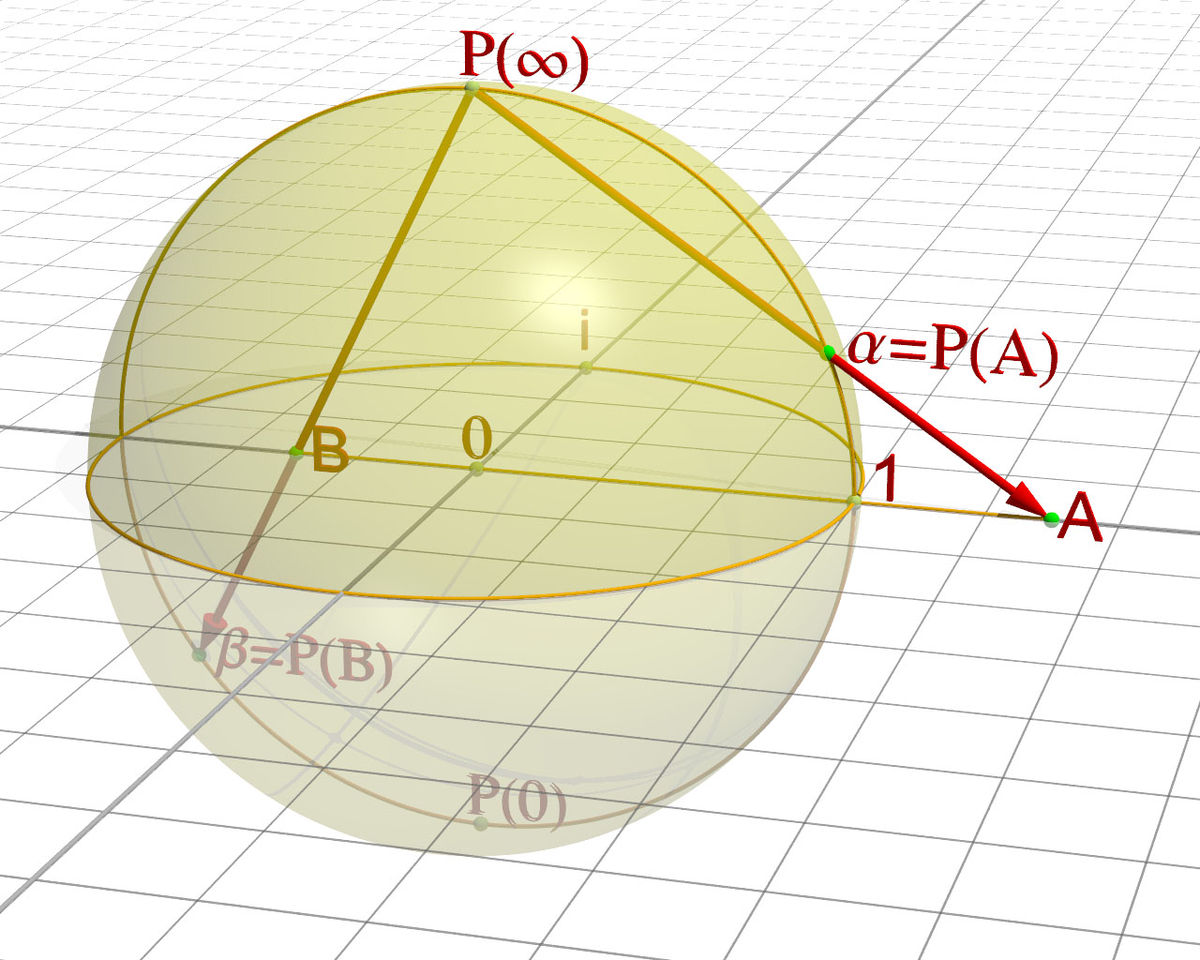
La projection stéréographique, par exemple sur le plan équatorial à partir du pôle Nord, permet de voir que la sphère privée d'un point est homéomorphe au plan. Inversement, on passe du plan à la sphère en ajoutant un point à l'infini", noté
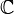
Remarque
Plus généralement, l'espace
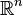
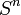
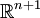
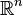
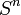
La droite projective complexe
C'est l'ensemble des "droites vectorielles" de
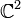
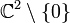
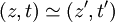

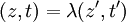
On la note
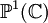
![[z,t]\,](https://static.techno-science.net/illustration/Definitions/autres/e/ed5a4fd52ab0feb3c41d285c262348cb_4e4b2dab77b8709ab2640c95178ee88c.png)
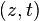
![[z,t]\,](https://static.techno-science.net/illustration/Definitions/autres/e/ed5a4fd52ab0feb3c41d285c262348cb_4e4b2dab77b8709ab2640c95178ee88c.png)
Remarquons aussi que
![\phi_1 : z\mapsto [z,1]](https://static.techno-science.net/illustration/Definitions/autres/8/83d883743c311240c069e33c1141fa90_d52753f5a3ffc07d1d2d95d3e2161f71.png)

![\mathbb P^1(\mathbb C)\setminus[1,0]](https://static.techno-science.net/illustration/Definitions/autres/d/dc3d4b98812b3d50f14557ae84507ef3_ecd308987809034b157299340d043bf6.png)
![\phi_2 : z\mapsto [1,z]](https://static.techno-science.net/illustration/Definitions/autres/2/27f270881cdcf95314eb676fd481d399_d979dd6903d57252e78f3fb2988c25ea.png)

![\mathbb P^1(\mathbb C)\setminus[0,1]](https://static.techno-science.net/illustration/Definitions/autres/9/960c2c09d60d8ef8366b54ca520b04bf_5f181657eb00b849c1785fb0eb6c7397.png)

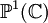
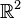
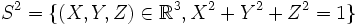
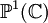
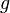
![g(X,Y,Z)=[X+iY,Z]\,](https://static.techno-science.net/illustration/Definitions/autres/6/65a5cab2f3a79e7553f7441007633aa1_4bd774d6d8986772bd333940acb9da0f.png)
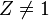
![g(X,Y,Z)=[Z,X-iY]\,](https://static.techno-science.net/illustration/Definitions/autres/0/03936b04d3cccc7a0eab6a523b5d0304_5285e7d3f39c0e8bd05716b6085d5ddb.png)
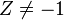
(ces deux définitions sont compatibles si
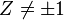
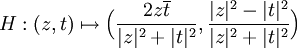
Homographies
On peut faire agir une matrice de
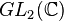
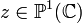
- si
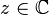
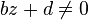
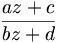
- si
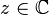
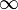
- si
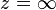
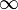
- si
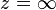
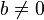
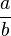
Une homographie est la bijection de la sphère de Riemann induite par l'action d'une matrice (on identifie souvent les deux); c'est même une fonction méromorphe.

















































