Glossaire topologique - Définition
Ceci est un glossaire de quelques termes utilisés en topologie.
Ce glossaire est divisé en deux parties. La première traite des concepts généraux, et la seconde liste différents types d'espaces topologiques. Dans ce glossaire, tous les espaces sont supposés topologiques.
Généralités
A
Accessible
- Un espace est accessible (ou T1) lorsque tous ses singletons sont fermés. Pour tout couple de points distincts, chacun d'eux possède un voisinage qui ne contient pas l'autre. En particulier, c'est un espace de Kolmogorov. Tout point d'un espace T1 est intersection de ses voisinages. Un espace E infini dont les ouverts non vides sont les complémentaires des parties finies (c'est-à-dire muni de la topologie cofinie) est T1 mais pas T2.
Adhérence
- Dans un espace topologique l'adhérence ou fermeture d'une partie est le plus petit fermé contenant celle-ci. Un point est dit adhérent à une partie s'il appartient à son adhérence.
B
Base dénombrable
Base d'ouverts
- Un ensemble d'ouverts est une base pour une topologie lorsque chaque ouvert de celle-ci est une union d'éléments de la base.
Base de voisinages
- Voir système fondamental de voisinages.
Boule
- Dans un espace métrique, la boule ouverte (respectivement fermée) de centre x et de rayon r (réel strictement positif) est l'ensemble des points situés à une distance de x strictement inférieure (respectivement inférieure ou égale) à r.
C
Complètement de Hausdorff
- Un espace est complètement de Hausdorff (ou T2½) lorsque deux points distincts admettent des voisinages dont les adhérences sont disjointes. En particulier, c'est un espace T2. L'ensemble


Complètement normal
- Un espace complètement normal (ou T5) est un espace séparé vérifiant : pour toutes parties A et B telles que l'adhérence de l'un n'intersecte pas l'autre, il existe deux ouverts disjoints U et V contenant respectivement A et B. Tout espace complètement normal est normal, T4
Complètement régulier
- Un espace séparé est complètement régulier (ou T3½) si pour tout fermé F et pour tout point x n'appartenant pas à F, F et {x} sont fonctionnellement séparés, i.e. il existe une fonction continue s'annulant sur F et valant 1 en x. Les espaces de Tychonoff sont réguliers.
- Une application d'un espace topologique dans un autre est continue lorsque l'image réciproque de chaque ouvert est un ouvert.
D
Dense
- Une partie dense d'un espace topologique est une partie dont l'adhérence est l'espace tout entier.
Dérivé
- Si P est une partie d'un espace topologique, son ensemble dérivé P' est l'ensemble de ses points d'accumulation.
Discrète
- Voir Topologie discrète
Distance
- Une distance définie sur un ensemble E est une application de E × E dans
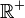
- d(x,y) = d(y,x) ;
- d(x,y) = 0 si et seulement si x=y ;
- d(x,z) ≤ d(x,y) + d(y,z).
E
Engendrée
- Voir Topologie engendrée
Espace à base dénombrable
- Espace topologique admettant une base d'ouverts dénombrable.
Espace métrique
- Un espace métrique est un couple (E,d), où E est un ensemble, et d une distance définie sur E.
- Un espace polonais est un espace séparable dont la topologie peut être définie par une distance qui en fait un complet.
Espace topologique
-
- C'est un ensemble E muni d'un sous-ensemble T de l'ensemble de ses parties qui vérifie :
- E lui-même et l'ensemble vide sont des éléments de T ;
- La réunion de toute famille d'éléments de T est un élément de T ;
- L'intersection de deux éléments de T est elle-même un élément de T.
- L'ensemble T est alors appelé la topologie mise sur E, et celles des parties de E qui appariennent à T sont appelées les ouverts de cette topologie.
F
Faiblement normal
- Un espace faiblement normal est un espace complètement régulier dont on peut séparer par deux ouverts disjoints deux fermés disjoints dont l'un est dénombrable.
Fermé
- Une partie d'un espace topologique est dite fermée lorsque son complémentaire est un ouvert.
Fermeture
- Voir Adhérence.
Fonctionnellement séparés
- Deux sous-ensembles A et B d'un espace topologique X sont dits fonctionnellement séparés lorsqu'il existe une fonction continue
![f : X \to [0,1]](https://static.techno-science.net/illustration/Definitions/autres/c/c218d8420c9856f71bdde71bd9f907e9_17938ed3dba2f773252d33620019b8ac.png)
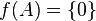
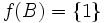
Fréchet
- Voir Accessible.
- La frontière d'une partie d'un espace topologique est le complémentaire de son intérieur dans son adhérence. C'est donc l'ensemble des points qui sont adhérents à la fois à cette partie et à son complémentaire.
G
Grossière
- Voir Topologie grossière.
H
Hausdorff
- Voir Séparé.
- On appelle homéomorphisme entre deux espaces topologiques X et Y toute bijection
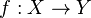
Homogène
- Un espace X est homogène si pour tout couple de points
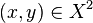
- Deux applications continues
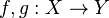
![H : X\times [0,1] \to Y](https://static.techno-science.net/illustration/Definitions/autres/e/e90fbf798237734541171ebfcd412898_a29a16e0ea3cd3c55e71d37817dbf3d8.png)
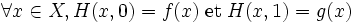
I
Induite
- Voir Topologie induite.
Intérieur
- L'intérieur d'une partie d'un espace topologique est le plus grand ouvert contenu dans cette partie. C'est aussi la réunion de tous les ouverts contenus dans cette partie, ou le complémentaire de l'adhérence de son complémentaire. Un point d'une partie lui est intérieur si et seulement s'il existe, inclus dans cette partie, un voisinage ouvert de ce point.
J
K
Kolmogorov
- Un espace est de Kolmogorov (ou T0) lorsque pour tout couple de points distincts, il existe un voisinage de l'un qui ne contient pas l'autre. L'espace E = {a,b} dont les ouverts sont
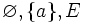
L
Localement fini
- Une famille de parties d'un espace topologique est dite localement finie lorsque chaque point possède un voisinage qui ne rencontre qu'un nombre fini d'éléments de la famille.
Localement métrisable
- Un espace est dit localement métrisable lorsque chaque point admet un voisinage métrisable.
M
Maigre
- Une partie d'un espace topologique est dite maigre lorsqu'elle est contenue dans une réunion dénombrable de fermés d'intérieur vide.
Métrique
- Voir Espace métrique.
Métrisabilité
- Un espace topologique est dit métrisable lorsque sa topologie peut être définie par une distance. Les espaces métrisables sont toujours séparés et paracompacts (et, par conséquence, normaux et de Tychonoff). Un espace à base dénombrable est métrisable si et seulement s'il est régulier d'après le lemme d'Urysohn.
Moins fine
- Voir Topologie moins fine.
N
Normal
- Un espace normal est un espace topologique dans lequel deux fermés disjoints possèdent des voisinages disjoints. Le lemme d'Urysohn garantit alors que ces deux fermés sont fonctionnellement séparés.
O
Ouvert
- Élement d'une topologie.
P
Parfait
- Un ensemble parfait d'un espace topologique est un fermé sans point isolé.
Parfaitement normal
- Un espace est parfaitement normal lorsqu'il est normal et tout fermé de l'espace est intersection dénombrable d'ouverts. Il est alors complètement normal.
Partition de l'unité
- Une partition de l'unité sur un espace topologique est un ensemble de fonctions continues à valeurs dans [0,1] telles que chaque point possède un voisinage sur lequel toutes les fonctions, sauf un nombre fini, sont identiquement nulles et telle que la somme des fonctions soit identiquement égale à 1.
Plus fine
- Voir Topologie plus fine.
Point d'accumulation
- Dans un espace topologique, un point d'accumulation d'une partie A est un point x adhérent à A - {x}.
Point isolé
- Dans un espace topologique séparé, un point isolé d'une partie A est un point x de A pour lequel il existe un voisinage qui ne rencontre A qu'au point x. Un point de A qui n'est pas isolé est un point d'accumulation de A.
Polonais
- Voir Espace polonais.
Prébase
- Un ensemble d'ouverts est une prébase pour une topologie lorsque l'ensemble des intersections finies d'éléments de cet ensemble est une base. On dit aussi que cette topologie est engendrée par la prébase.
Produit
- Voir Topologie produit.
Q
Quotient
- Voir Topologie quotient.
R
- Un recouvrement K est un raffinement du recouvrement L lorsque chaque élément de K est inclus dans un élément de L.
Rare
- Une partie d'un espace topologique est dite rare lorsque son adhérence est d'intérieur vide. De manière équivalente, le complémentaire de son adhérence est dense.
Recouvrement
- Une famille
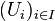
Régulier
- Un espace séparé est régulier (ou T3) lorsque pour tout fermé F et pour tout point x n'appartenant pas à F, x et F admettent des voisinages disjoints. En particulier, c'est un espace T2½. Tout fermé est l'intersection de ses voisinages fermés. Tout point admet une base de voisinages fermés.
S
Séparable
- Un espace séparable est un espace qui admet une partie dense dénombrable.
Séparé
- Un espace est séparé (ou T2) lorsque deux points distincts admettent des voisinages disjoints. En particulier, c'est un espace T1. Tout point d'un espace T2 est intersection de ses voisinages fermés. On trouvera dans l'article espace séparé un exemple d'espace T2 mais non T2½.
Sous-recouvrement
- Un recouvrement K est un sous-recouvrement du recouvrement L lorsque chaque élément de K appartient à L.
Système fondamental de voisinages
- Un ensemble
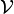
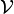
T
T0
- Voir Kolmogorov.
T1
- Voir Accessible.
T2
- Voir Séparé.
T2½
- Voir Complètement de Hausdorff
T3
- Voir Régulier.
T3½
- Voir Complètement régulier
T4
- Un espace est T4 lorsqu'il est séparé et normal.
T5
- Voir Complètement normal.
Topologie
- Voir Espace topologique.
Topologie discrète
- Topologie dans laquelle tous les ensembles sont ouverts. C'est la plus fine de toutes les topologies.
Topologie engendrée (par un ensemble d'ouverts)
- Topologie dont les ouverts sont les réunions quelconques d'intersections finies d'ouverts de l'ensemble. L'ensemble d'ouverts donné constitue une prébase de la topologie.
Topologie grossière
- Topologie dont les seuls ouverts sont l'ensemble vide et l'espace tout entier. C'est la moins fine de toutes les topologies.
Topologie induite
- La topologie induite sur une partie A d'un espace topologique (E,T) est la topologie la moins fine sur A rendant continue l'injection canonique
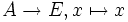
Topologie moins fine
- Soient T, T' deux topologies sur le même ensemble E. La topologie T est moins fine que la topologie T' si tout ouvert de T est ouvert de T'. Cela équivaut à la continuité de l'application identique de (E,T') dans (E,T).
Topologie plus fine
- Soient T, T' deux topologies sur le même ensemble E. La topologie T est plus fine que la topologie T' si tout ouvert de T' est ouvert de T. Cela équivaut à la continuité de l'application identique de (E,T) dans (E,T').
Topologie produit
- Si (Ei ,Ti), i appartenant à I, est une famille d'espaces topologiques, la topologie produit définie sur
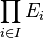
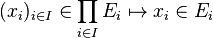
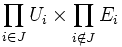
Topologie quotient
- Si (E,T) est un espace topologique et R une relation d'équivalence sur E, la topologie quotient définie sur l'ensemble quotient E/R est la plus fine rendant continue la projection canonique, qui à x de E, associe sa classe d'équivalence dans E/R.
Topologique
- Voir Espace topologique.
Tychonoff
- Voir Complètement régulier
U
Uniformisable
- Voir Complètement régulier
V
Valeur d'adhérence
- Dans un espace métrique, une valeur d'adhérence d'une suite est la limite d'une sous-suite. C'est un point tel que tout voisinage de ce point contient une infinité de termes de la suite.
Voisinage
- Un voisinage d'une partie S d'un espace topologique E est un ensemble contenant un ouvert contenant S ; en particulier, un voisinage ouvert de S est un ouvert contenant cette partie. Un voisinage d'un point p est un voisinage du singleton {p}.
Espaces topologiques
Les espaces topologiques peuvent être classés en fonction de la séparation entre leur points, de leur compacité, leur taille ou leur connexité.
Axiomes de séparation
Les axiomes de séparation permettent d'imposer des restriction sur les espaces topologiques. Certains des termes employés ici peuvent avoir été définis autrement dans la littérature ancienne ; voir l'histoire des axiomes de séparation.
Note : l'expression " axiome de séparation " en topologie ne doit pas être confondue avec l'axiome de séparation de la théorie des ensembles).
T0 ou de Kolmogorov
- Un espace est T0 lorsque pour tout couple de points distincts, il existe un voisinage de l'un qui ne contient pas l'autre. L'espace E = {a,b} dont les ouverts sont
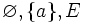
T1 ou accessible ou de Fréchet
- Un espace est T1 lorsque tous ses singletons sont fermés. Pour tout couple de points distincts, chacun d'eux possède un voisinage qui ne contient pas l'autre. En particulier, c'est un espace de Kolmogorov. Tout point d'un espace T1 est intersection de ses voisinages. Un espace E infini dont les ouverts non vides sont les complémentaires des parties finies (c'est-à-dire muni de la topologie cofinie) est T1 mais pas T2.
T2 ou de Hausdorff ou séparé
- Un espace est séparé lorsque deux points distincts admettent des voisinages disjoints. En particulier, c'est un espace T1. Tout point d'un espace T2 est intersection de ses voisinages fermés. On trouvera dans l'article espace séparé un exemple d'espace T2 mais non T2½.
T2½ ou complètement de Hausdorff
- Un espace est T2½ lorsque deux points distincts admettent des voisinages dont les adhérences sont disjointes. En particulier, c'est un espace T2. L'ensemble


T3 ou régulier
- Un espace séparé est régulier lorsque pour tout fermé F et pour tout point x n'appartenant pas à F, x et F admettent des voisinages disjoints. En particulier, c'est un espace T2½. Tout fermé est l'intersection de ses voisinages fermés. Tout point admet une base de voisinages fermés.
T3½ ou de Tychonoff ou complètement régulier ou uniformisable
- Un espace séparé est complètement régulier si pour tout fermé F et pour tout point x n'appartenant pas à F, F et {x} sont fonctionnellement séparés, i.e. il existe une fonction continue s'annulant sur F et valant 1 en x. Les espaces de Tychonoff sont réguliers.
Faiblement normal
- Un espace faiblement normal est un espace complètement régulier dont on peut séparer par deux ouverts disjoints deux fermés disjoints dont l'un est dénombrable.
Normal
- Un espace normal est un espace topologique dans lequel deux fermés disjoints possèdent des voisinages disjoints. Le lemme d'Urysohn garantit alors que ces deux fermés sont fonctionnellement séparés.
T4
- Un espace est T4 lorsqu'il est séparé et normal.
T5 ou complètement normal
- Un espace est complètement normal est un espace séparé vérifiant : pour toutes parties A et B telles que l'adhérence de l'un n'intersecte pas l'autre, il existe deux ouverts disjoints U et V contenant respectivement A et B. Tout espace complètement normal est normal, T4
Parfaitement normal
- Un espace est parfaitement normal lorsqu'il est normal et tout fermé de l'espace est intersection dénombrable d'ouverts. Il est alors complètement normal.
Axiomes de recouvrement
Un recouvrement ouvert est un ensemble d'ouverts tel que leur union recouvre l'espace.
Paracompact
- Un espace topologique est paracompact lorsque tout recouvrement ouvert admet un raffinement localement fini. Les espaces séparés paracompacts sont normaux.
Lindelöf
- Un espace est de Lindelöf lorsque tout recouvrement ouvert admet un sous-recouvrement dénombrable.
Quasi-compact
- Un espace est quasi-compact lorsque tout recouvrement ouvert admet un sous-recouvrement fini.
Compact
- Un espace est compact lorsqu'il est quasi-compact et séparé. (Le terme compact est parfois utilisé pour ce que nous avons appelé ici quasi-compact, rendant nécessaire l'utilisation de compact Hausdorff pour ce que nous appelons ici un compact.)
Localement compact
- Un espace est localement compact si chaque point admet un système fondamental de voisinages compacts. Les espaces séparés localement compacts sont de Tychonoff.
Relativement compact
- Un sous-ensemble d'un espace topologique est relativement compact lorsque son adhérence est compacte.
Connexité
Connexe
- Un espace est connexe lorsqu'il n'est pas l'union disjointe de deux ouverts non vides.
Localement connexe
- Un espace est localement connexe lorsque chaque point admet un système fondamental de voisinages connexes.
Composante connexe
- La composante connexe contenant un point est le plus grand ensemble connexe contenant ce point. C'est l'union de tous les ensembles connexes contenant ce point.
Totalement discontinu
- Un espace est totalement discontinu lorsque toutes les composantes connexes sont des singletons.
Connexe par arcs
- Un espace X est connexe par arcs lorsque pour tout couple de points
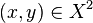
![p:[0,1]\to X](https://static.techno-science.net/illustration/Definitions/autres/c/c2908a2ef3893f387f5f8042ee82d2b9_cffa9b8b9065eeac414639d059beebc5.png)
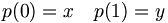
Localement connexe par arcs
- Un espace est localement connexe par arcs lorsque chaque point admet un système fondamental de voisinages connexes par arcs. Un espace localement connexe par arcs est connexe si et seulement s’il est connexe par arcs.
Simplement connexe
- Un espace est simplement connexe lorsqu'il est connexe par arcs et toute application continue
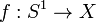
Contractile
- Un espace X est contractile lorsque l' application identité de X est homotope à une application constante. Les espaces contractiles sont toujours simplement connexes.

















































