Théorème de Baire - Définition
Un espace topologique est dit de Baire (du nom du mathématicien René Baire) si toute intersection dénombrable d'ouverts denses est dense. De façon équivalente, un espace topologique est de Baire si une union dénombrable de fermés d'intérieur vide est d'intérieur vide.
Théorème de Baire (dit aussi Lemme de Baire)
- Un espace topologique localement compact E est de Baire;
- Un espace métrique complet (E,d) (notamment un espace de Banach) est de Baire.
Dans ce qui suit, int(A) désigne l'intérieur d'une partie A de E.
- Soit
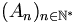
rencontre cet ouvert. Comme E est localement compact, on peut sans perte de généralité supposer que cet ouvert est relativement compact (ie d'adhérence compacte).
Puisque A1 est dense, il rencontre V : soit
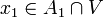
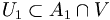
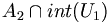
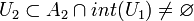
En itérant cette construction, on obtient une suite de compacts
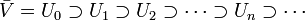
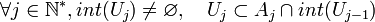
Or,
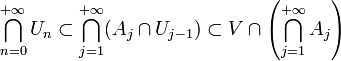
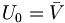
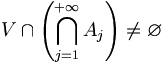
- Dans le cas où E est un espace métrique complet, le raisonnement est analogue. Soit V une boule fermée centrée en
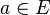

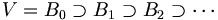
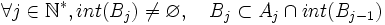
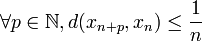
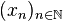
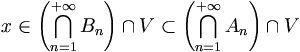
Quelques applications du lemme de Baire
- Analyse fonctionnelle
- Théorèmes de l'application ouverte, du graphe fermé, de l'isomorphisme de Banach
- Théorème de Banach-Steinhaus
- Théorème de la limite simple de Baire
- Connexité du tipi de Cantor
- Théorème de superposition de Kolmogorov
- Caractérisation des polynômes réels : Si f est une fonction
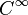
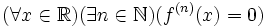
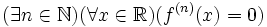
- La boite à Baire (BwataBaire) est un wiki qui se propose de recenser diverses applications du lemme de Baire, et de réfléchir aux relations qu'il entretient avec des phénomènes similaires (uniformisation...).