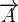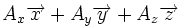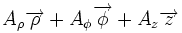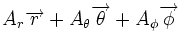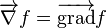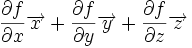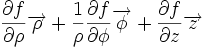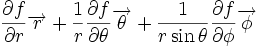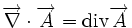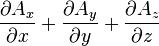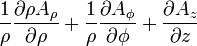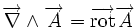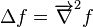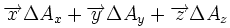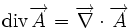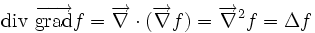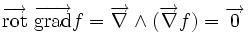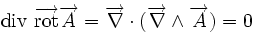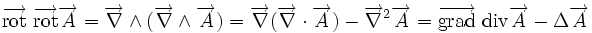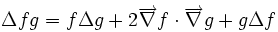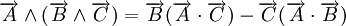Nabla - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs est disponible ici.

Article d'analyse vectorielle

Objets d'étude
Champ vectoriel	Champ scalaire
Équation aux dérivées partielles
de Laplace – de Poisson
Opérateurs
Nabla	Gradient
Rotationnel	Divergence
Laplacien scalaire	Bilaplacien
Laplacien vectoriel	D'alembertien
Théorèmes
de Green	de Stokes
de Helmholtz	de flux-divergence
du gradient	du rotationnel

Nabla, noté $\nabla$ , est un symbole mathématique pouvant aussi bien désigner le gradient d'une fonction en analyse qu'une connexion de Koszul en géométrie différentielle. Les deux notions sont évidemment reliées, ce qui explique l'utilisation d'un même symbole. En physique, il est utilisé de manière informelle en dimension 3 pour représenter aisément la divergence ( $\nabla\cdot A$ ), le rotationnel ( $\nabla\times A$ ) et le laplacien vectoriel ( $ΔA = \nabla² A$ ) d'un champ vectoriel $A$ , ainsi que le gradient ( $\nablaf$ ) et le laplacien ( $Δf = \nabla²f$ ) d'un champ scalaire $f$ . Ces notions sont fondamentales en physique, notamment en électromagnétisme et en hydrodynamique.

Origine historique

La forme de Nabla vient d'un delta ( $Δ$ ) renversé, à cause d'une utilisation comparable (calcul différentiel), elle a été introduite par Peter Guthrie Tait en 1867. D'abord surnommé avec malice " atled " (delta à l'envers) par James Maxwell, le nom Nabla lui fut donné par Tait sur l'avis de William Robertson Smith, en 1870, par analogie de forme avec une harpe grecque qui dans l'antiquité portait ce nom.

Opération	Coordonnées cartésiennes (x,y,z)	Coordonnées cylindriques (ρ,?,z)	Coordonnées sphériques (r,θ,?)
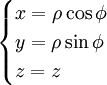
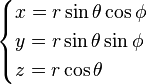
Définition des coordonnées		$\begin{cases} x = \rho\cos\phi \\ y = \rho\sin\phi \\ z = z \end{cases}$	$\begin{cases} x = r\sin\theta\cos\phi \\ y = r\sin\theta\sin\phi \\ z = r\cos\theta \end{cases}$
$\overrightarrow A$	$A_x\overrightarrow x + A_y\overrightarrow y + A_z\overrightarrow z$	$A_\rho\overrightarrow \rho + A_\phi\overrightarrow \phi + A_z\overrightarrow z$	$A_r\overrightarrow r + A_\theta\overrightarrow \theta + A_\phi\overrightarrow \phi$
$\overrightarrow\nabla f = \overrightarrow{\mathrm{grad}} f$	${\partial f \over \partial x}\overrightarrow x + {\partial f \over \partial y}\overrightarrow y + {\partial f \over \partial z}\overrightarrow z$	${\partial f \over \partial \rho}\overrightarrow \rho + {1 \over \rho}{\partial f \over \partial \phi}\overrightarrow \phi + {\partial f \over \partial z}\overrightarrow z$	${\partial f \over \partial r}\overrightarrow r + {1 \over r}{\partial f \over \partial \theta}\overrightarrow \theta + {1 \over r\sin\theta}{\partial f \over \partial \phi}\overrightarrow \phi$
$\overrightarrow\nabla\cdot\overrightarrow A = \mathrm{div} \overrightarrow{A}$	${\partial A_x \over \partial x} + {\partial A_y \over \partial y} + {\partial A_z \over \partial z}$	${1 \over \rho}{\partial \rho A_\rho \over \partial \rho} + {1 \over \rho}{\partial A_\phi \over \partial \phi} + {\partial A_z \over \partial z}$	${1 \over r^2}{\partial r^2 A_r \over \partial r} + {1 \over r\sin\theta}{\partial A_\theta\sin\theta \over \partial \theta} + {1 \over r\sin\theta}{\partial A_\phi \over \partial \phi}$
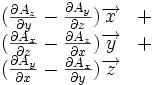
$\overrightarrow\nabla \wedge \overrightarrow A = \overrightarrow{\mathrm{rot}} \overrightarrow{A}$	$\begin{matrix} ({\partial A_z \over \partial y} - {\partial A_y \over \partial z}) \overrightarrow x & + \\ ({\partial A_x \over \partial z} - {\partial A_z \over \partial x}) \overrightarrow y & + \\ ({\partial A_y \over \partial x} - {\partial A_x \over \partial y}) \overrightarrow z & \ \end{matrix}$	$\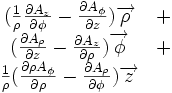begin{matrix} ({1 \over \rho}{\partial A_z \over \partial \phi} - {\partial A_\phi \over \partial z}) \overrightarrow \rho & + \\ ({\partial A_\rho \over \partial z} - {\partial A_z \over \partial \rho}) \overrightarrow \phi & + \\ {1 \over \rho}({\partial \rho A_\phi \over \partial \rho} - {\partial A_\rho \over \partial \phi}) \overrightarrow z & \ \end{matrix}$	$\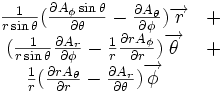begin{matrix} {1 \over r\sin\theta}({\partial A_\phi\sin\theta \over \partial \theta} - {\partial A_\theta \over \partial \phi}) \overrightarrow r & + \\ ({1 \over r\sin\theta}{\partial A_r \over \partial \phi} - {1 \over r}{\partial r A_\phi \over \partial r}) \overrightarrow \theta & + \\ {1 \over r}({\partial r A_\theta \over \partial r} - {\partial A_r \over \partial \theta}) \overrightarrow \phi & \ \end{matrix}$
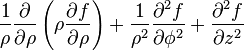
$\Delta f = \overrightarrow\nabla^2 f$	${\partial^2 f \over \partial x^2} + {\partial^2 f \over \partial y^2} + {\partial^2 f \over \partial z^2}$	${1 \over \rho}{\partial \over \partial \rho}\left(\rho {\partial f \over \partial \rho}\right) + {1 \over \rho^2}{\partial^2 f \over \partial \phi^2} + {\partial^2 f \over \partial z^2}$	${1 \over r^2}{\partial \over \partial r}\left(r^2 {\partial f \over \partial r}\right) + {1 \over r^2\sin\theta}{\partial \over \partial \theta}\left(\sin\theta {\partial f \over \partial \theta}\right) + {1 \over r^2\sin\theta}{\partial^2 f \over \partial \phi^2}$
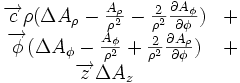
$\Delta \overrightarrow A = \overrightarrow\nabla^2 \overrightarrow A$	$\overrightarrow x\Delta A_x + \overrightarrow y\Delta A_y + \overrightarrow z\Delta A_z$	$\begin{matrix} \overrightarrow c \rho(\Delta A_\rho - {A_\rho \over \rho^2} - {2 \over \rho^2}{\partial A_\phi \over \partial \phi}) & + \\ \overrightarrow \phi(\Delta A_\phi - {A_\phi \over \rho^2} + {2 \over \rho^2}{\partial A_\rho \over \partial \phi}) & + \\ \overrightarrow z \Delta A_z & \ \end{matrix}$	$\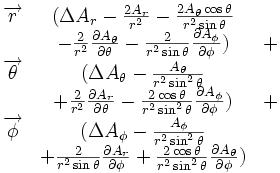begin{matrix} \overrightarrow r & (\Delta A_r - {2 A_r \over r^2} - {2 A_\theta\cos\theta \over r^2\sin\theta} \\ \ & - {2 \over r^2}{\partial A_\theta \over \partial \theta} - {2 \over r^2\sin\theta}{\partial A_\phi \over \partial \phi}) & + \\ \overrightarrow \theta & (\Delta A_\theta - {A_\theta \over r^2\sin^2\theta} \\ \ & + {2 \over r^2}{\partial A_r \over \partial \theta} - {2 \cos\theta \over r^2\sin^2\theta}{\partial A_\phi \over \partial \phi}) & + \\ \overrightarrow \phi & (\Delta A_\phi - {A_\phi \over r^2\sin^2\theta} \\ \ & + {2 \over r^2\sin\theta}{\partial A_r \over \partial \phi} + {2 \cos\theta \over r^2\sin^2\theta}{\partial A_\theta \over \partial \phi}) & \ \end{matrix}$
Règles de calcul non évidentes: $\mathrm{div}\overrightarrow {A}=\overrightarrow \nabla\cdot\overrightarrow {A}$ $\operatorname{div}\ \overrightarrow{\operatorname{grad}} f = \overrightarrow \nabla \cdot (\overrightarrow \nabla f) = \overrightarrow \nabla^2 f = \Delta f$ (laplacien) $\overrightarrow{\operatorname{rot}}\ \overrightarrow{\operatorname{grad}} f = \overrightarrow \nabla \wedge (\overrightarrow \nabla f) = \overrightarrow 0$ $\operatorname{div}\ \overrightarrow{\operatorname{rot}} \overrightarrow {A} = \overrightarrow \nabla \cdot (\overrightarrow \nabla \wedge \overrightarrow {A}) = 0$ $\overrightarrow{\operatorname{rot}}\ \overrightarrow{\operatorname{rot}} \overrightarrow {A} = \overrightarrow \nabla \wedge (\overrightarrow \nabla \wedge \overrightarrow {A}) = \overrightarrow \nabla (\overrightarrow \nabla \cdot \overrightarrow {A}) - \overrightarrow \nabla^2 \overrightarrow {A} = \overrightarrow{\operatorname{grad}}\ \operatorname{div} \overrightarrow A - \Delta \overrightarrow A$ $\Delta f g = f \Delta g + 2 \overrightarrow \nabla f \cdot \overrightarrow \nabla g + g \Delta f$ Formule de Lagrange pour le produit vectoriel : $\overrightarrow {A} \wedge (\overrightarrow {B} \wedge \overrightarrow {C}) = \overrightarrow {B} (\overrightarrow {A} \cdot \overrightarrow {C}) - \overrightarrow {C} (\overrightarrow {A} \cdot \overrightarrow {B})$

Nabla - Définition

Origine historique

Utilisation en analyse vectorielle