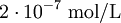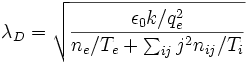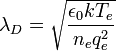Longueur de Debye - Définition
En physique des plasmas, la longueur de Debye, en référence au chimiste Peter Debye, est l'échelle de longueur sur laquelle les charges électriques (par exemple les électrons) écrantent le champ électrostatique dans un plasma ou un autre conducteur. Autrement dit, la longueur de Debye est la distance en dessus de laquelle une séparation significative des charges peut avoir lieu.
La longueur de Debye apparait aussi dans la théorie des solutions d'électrolyte ; elle y définit la longueur sur laquelle les ions présents en solution font écran au champ électrique, généré par exemple par une paroi chargée ou un colloïde. De manière équivalente, la longueur de Debye caractérise l'épaisseur de la double couche électrique, nom donné à la couche diffuse d'ions qui apparait en vis-à-vis d'une surface chargée, porteuse d'une charge nette opposée à celle de la surface.
Quelques exemples
Dans l'espace, la densité d'électrons dans les plasmas est relativement faible, ce qui permet d'obtenir les ordres de grandeurs macroscopiques pour la longueur de Debye (voir table) :
| Plasma | Densité ne(m-3) |
Température des électrons T(K) |
Champ magnétique B(T) |
Longueur de Debye λD(m) |
|---|---|---|---|---|
| Décharge dans un gaz | 1016 | 4 | -- | 10-4 |
| Tokamak | 1020 | 108 | 10 | 10-4 |
| Ionosphère | 1012 | 103 | 10-5 | 10-3 |
| Magnétosphère | 107 | 107 | 10-8 | 102 |
| Noyau solaire | 1032 | 107 | -- | 10-11 |
| Vent solaire | 106 | 105 | 10-9 | 10 |
| Milieu interstellaire | 105 | 104 | 10-10 | 10 |
| Milieu intergalactique | 1 | 106 | -- | 105 |
http://www.pma.caltech.edu/Courses/ph136/yr2002/
La longueur de Debye dans un plasma
|
|
où:
λD est la longueur de Debye,
ε0 est la permittivité du vide,
k est la constante de Boltzmann,
qe est la charge d'un électron,
Te et Ti sont respectivement les températures des électrons et des ions,
ne est la densité d'électrons,
nij est la densité d'atomes i ayant une charge jqe
Le terme ionique est souvent négligé (lorsque la température des ions est négligeable devant celle des électrons}. La formule se simplifie alors en :
|
|
La longueur de Debye dans un électrolyte
Expression
En présence de n types d'ions de charge qi (
) dans la solution d'électrolyte, la longueur de Debye est donnée par :
,
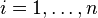
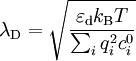
où :
est la permittivité diélectrique du solvant (
étant la permittivité diélectrique du vide, et 
la permittivité relative du solvant : dans l'eau à température ambiante 
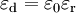
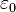
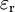
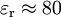
) ;- T est la température exprimée en Kelvin ; kB est la constante de Boltzmann qui relie température et énergie thermique ;
est la concentration en ions de charge qi loin de la charge écrantée, là où le champ électrique est nul.
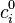
Cette expression de la longueur de Debye apparait lors de la résolution de l'équation de Poisson-Boltzmann, qui décrit l'écrantage d'une charge par les (micro)ions dans une solution d'électrolyte.
Dans le cas d'un électrolyte monovalent comme le chlorure de sodium (NaCl, sel de cuisine) ou le chlorure de potassium (KCl) :
,
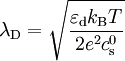
où 
est la concentration en électrolyte de la solution.
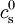
Valeurs typiques
Dans une solution aqueuse de sel monovalent (par exemple : sel de cuisine dissous dans de l'eau) à température ambiante (environ 20 °C), la longueur de Debye ne dépend plus que de la concentration en sel cs, exprimée en mol/L :
.
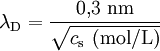
La longueur de Debye diminue lorsque la concentration en sel augmente.
Dans l'eau pure (situation extrêmement difficile à réaliser experimentalement), l'auto-dissociation de l'eau donne lieu à la présence d'ions H + et OH − , avec une concentration de 
. Ainsi, même dans la situation la plus idéale, le champ électrique sera écranté dans l'eau sur une distance de l'ordre de 700 nm, inférieure au micron. Pour des concentrations en sel significatives, la longueur de Debye varie de quelques dizaines de nanomètres à une fraction de nanomètre.