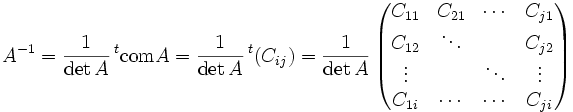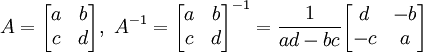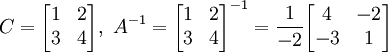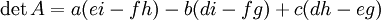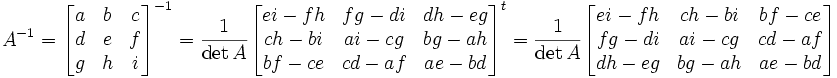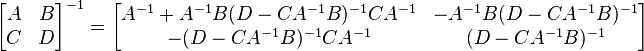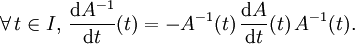Matrice inversible - Définition
En mathématiques et plus particulièrement en algèbre linéaire, une matrice carrée A d'ordre n est dite inversible ou régulière ou encore non singulière, s'il existe une matrice B d'ordre n telle que
- AB = BA = In,
où In désigne la matrice unité d'ordre n. La multiplication est la multiplication ordinaire des matrices. Dans ce cas, la matrice B est unique et est appelée la matrice inverse de A, et est notée A−1.
Une matrice carrée qui n'est pas inversible est dite non inversible ou singulière. Tandis que dans les cas usuels, ces matrices sont à coefficients réels ou complexes, toutes ces définitions peuvent être données pour des matrices à coefficients dans un corps (et plus généralement dans un anneau) quelconque.
Théorème des matrices inversibles
Soit A une matrice carrée d'ordre n à coefficients dans un corps



- A est inversible,
- A est équivalente à la matrice unité In d'ordre n,
- A possède n pivots,
- le déterminant de A est non nul : det (A) ≠ 0,
- 0 n'est pas valeur propre de A,
- le rang de A est égal à n,
- le système homogène AX = 0 a pour unique solution X = 0,
- pour tout b dans
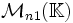
- pour tout b dans
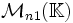
- pour tout b dans
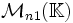
- les colonnes de A, considérées comme des vecteurs de
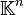
- les colonnes de A, considérées comme des vecteurs de
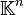
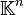
- les colonnes de A, considérées comme des vecteurs de
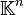
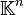
- l'endomorphisme canoniquement associé à A (c’est-à-dire l'application linéaire de
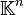
- l'endomorphisme can(A) canoniquement associé à A est surjectif,
- l'endomorphisme can(A) canoniquement associé à A est bijectif,
- la matrice A est inversible à gauche, c'est-à-dire qu'il existe une matrice B carrée d'ordre n telle que BA = In,
- la matrice A est inversible à droite, c'est-à-dire qu'il existe une matrice B carrée d'ordre n telle que AB = In,
- la transposée tA de A est inversible,
- il existe un polynôme annulateur de A dont 0 n'est pas racine,
- 0 n'est pas racine du polynôme minimal de A.
Plus généralement, une matrice carrée à coefficients dans un anneau commutatif unifère est inversible si et seulement si son déterminant est inversible dans cet anneau.
Autres propriétés et résultats
La matrice inverse d'une matrice inversible A est elle-même inversible, et
- (A−1)−1 = A
Le produit de deux matrices inversibles A et B (de même ordre) est une matrice inversible et son inverse est donné par la relation suivante (on remarquera que l'ordre des matrices est inversé)
- (AB)−1 = B−1A−1
Le produit d'un scalaire non nul k et d'une matrice inversible A est inversible, et son inverse est égal au produit de l'inverse de ce scalaire et de l'inverse de cette matrice.
- (kA)−1 = k−1A−1
Des deux premières de ces propriétés, il résulte que l'ensemble des matrices carrées inversibles d'ordre n constitue un groupe multiplicatif (dont l'élément neutre est la matrice unité d'ordre n); on l'appelle groupe général linéaire et on le note habituellement
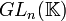

En général, " presque toutes " les matrices carrées d'ordre n sont inversibles. Sur le corps des nombres réels, cela peut être formulé de façon plus précise: l'ensemble des matrices non inversibles, considéré comme sous-ensemble de
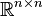
Méthodes d'inversion
Avant de décrire les méthodes usuelles d'inversion, notons qu'en pratique, il n'est pas nécessaire de calculer l'inverse d'une matrice pour résoudre un système d'équations linéaires. Il est toutefois nécessaire que la matrice considérée soit inversible. Des méthodes de décomposition comme la décomposition LU sont beaucoup plus rapide que l'inversion.
Élimination de Gauss-Jordan
Méthode des cofacteurs
L'inverse d'une matrice A s'écrit sous une forme très simple à l'aide de la matrice complémentaire tcomA
où detA est le déterminant de A, comA est la comatrice de A et tA est la matrice transposée de A.
Cette écriture permet un calcul aisé de l'inverse d'une matrice de petite dimension. Pour des matrices de plus grande dimensions, cette méthode essentiellement récursive devient inefficace.
Inversion des matrices 2 x 2
L'équation des cofacteurs ci-dessus permet de calculer l'inverse des matrices de dimensions 2 x 2 : si
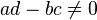
EXEMPLE
(M.Paris)
Inversion des matrices 3 x 3
De même, l'inverse d'une matrice de dimensions 3 x 3 s'écrit:
Inversion par bloc
L'inverse d'une matrice peut également être calculé par bloc, en utilisant la formule analytique suivante:
où A, B, C et D sont des blocs de taille arbitraire. Cette méthode peut se révéler avantageuse, par exemple, si A est diagonale et si son complément de Schur (D − CA − 1B) est une matrice de petite dimension, puisque ce sont les seules matrices à inverser.
Cette technique a été inventée par Volker Strassen, connu également pour l'algorithme de Strassen sur le produit matriciel rapide.
Dérivée de l'inverse d'une matrice
Soient un intervalle I (d'intérieur non vide) de

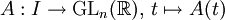
Alors la fonction matricielle
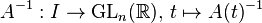
Cette relation découle de l'identité
-
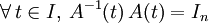
Généralisations
Certaines des propriétés des matrices inverses sont aussi vérifiées par les matrices pseudo-inverses qui peuvent être définies pour n'importe quelle matrice, même pour celles qui ne sont pas carrées.