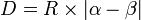Distance angulaire - Définition
La distance angulaire est la plus petite distance entre deux points d'un cercle. Généralisée en trois dimensions, elle revient au problème de la distance du grand cercle. Le périmètre d'un cercle peut être considéré comme une longueur (surface de dimension 1) : un point du cercle ne possède donc qu'une seule propriété, l'angle, noté α.
Soit deux points, A (angle α) et B (angle β), d'un cercle de rayon R, alors la distance angulaire entre ces deux points est :