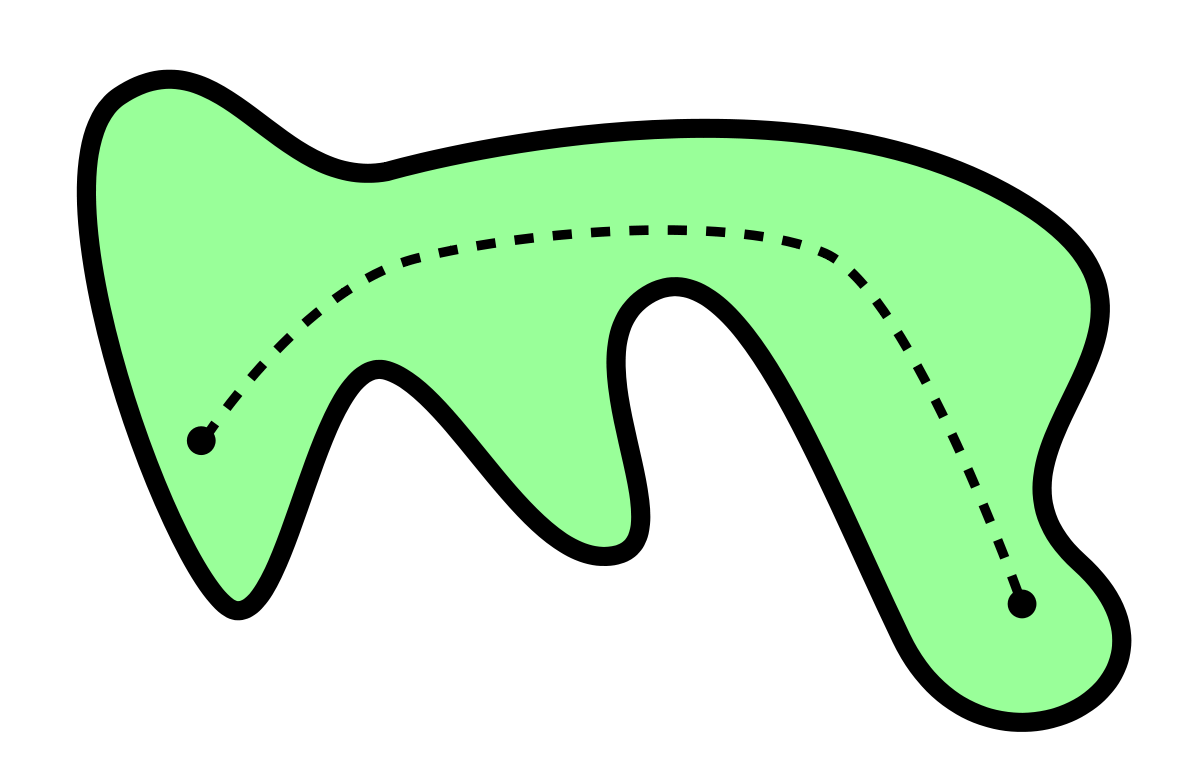
Connexité par arcs - Définition
La notion topologique de connexité par arcs est un raffinement de la notion de connexité. Un espace topologique est dit connexe par arcs si deux points quelconques peuvent toujours être reliés par un chemin. En fait, la connexité est la notion fondamentale. Mais la connexité par arcs est plus intuitive, et se trouve être très souvent la meilleure façon de prouver la connexité.
Chemins
Avant de définir la connexité par arcs il faut définir ce qu'on appelle " relier par un chemin ". Selon le cadre où l'on se trouve on peut considérer des chemins particuliers.
Chemins dans un espace topologique
Si
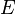
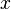
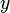
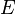
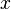
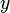
![\gamma : [0,1] \rightarrow E \,\!](https://static.techno-science.net/illustration/Definitions/autres/d/db93627744bbaf0fa6ed607653ec15fe_df9a7f83eb7a9907a9697735a41b767f.png)
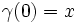
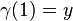
On dit que
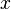
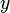
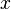
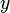
Propriété : La relation "
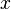
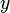
-
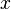
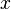
- (grâce au chemin constant
![\forall t \in [0,1],\, \gamma(t)=x \,\!](https://static.techno-science.net/illustration/Definitions/autres/a/a95f2f210115ea69e6d42d217380782d_964c3067e93abf18190834b4932c7447.png)
- si
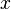
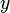
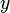
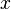
- (grâce au chemin opposé
![\forall t \in [0,1],\, \bar{\gamma}(t) = \gamma (1-t)\,\!](https://static.techno-science.net/illustration/Definitions/autres/c/c69388f16ff9cb7340c5113fd6761056_136c48f5bc543d093559174fb88db44a.png)
- si
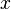
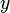
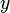
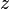
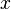
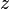
- (si
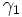
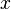
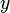
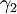
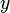
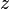
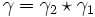
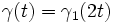
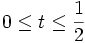
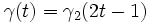
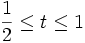
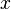
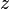
Chemins dans un espace vectoriel normé
Dans le cas où l'espace ambiant
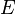
- Chemins rectilignes : un chemin est dit rectiligne si et seulement il peut s'écrire
![\forall t \in [0,1],\, \gamma(t) = x + t \vec{u} \,\!](https://static.techno-science.net/illustration/Definitions/autres/c/cd1c3897dd786ab2dabf5c60e0f6b131_0d77d5b9c0151aeae20387c9237c60cd.png)
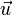
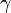
- Chemins polygonaux : un chemin est dit polygonal si et seulement s’il s'écrit comme un composé d'un nombre fini de chemins rectilignes. Par exemple, un trajet dans Manhattan est un chemin polygonal.
- Chemins de classe
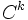
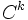
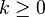
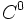
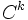
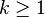
![\forall t \in ]0,1[ ,\, \gamma ' (t) \neq 0 \,\!](https://static.techno-science.net/illustration/Definitions/autres/d/d94a2e9637a74383207ad5cc740fedf2_ac589ba1e70fe4097722ba78d1ad1a84.png)
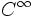
Connexité par arcs
Ces différents types de chemins vont permettre de définir différents types de connexité par arcs selon les cas.
Définition
Un espace topologique
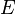
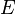
Une partie
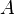
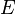
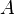
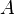
Une partie
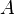
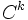
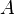
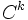
La connexité par arcs rectilignes correspond à la convexité.