Adhérence (mathématiques) - Définition

Définitions

En topologie, l'adhérence d'une partie X d'un espace topologique E est le plus petit ensemble fermé de E qui contienne X.

L'existence d'un tel fermé est claire : il existe au moins un fermé contenant X, à savoir l'espace E lui-même ; d'autre part, l'intersection de tous les fermés contenant X est un fermé contenant X, et est le plus petit ayant cette propriété.

L'adhérence de X est aussi appelée fermeture de X et se note souvent .

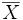
On dit d'un point x de E qu'il est adhérent à X lorsque tout voisinage de x rencontre X.

L'adhérence de X est égale à l'ensemble des points qui lui sont adhérents.

En effet :

1. Si le point x de E est adhérent à X, il ne peut appartenir à l'ouvert , car celui-ci serait alors un voisinage de x ne rencontrant pas X ; donc il appartient à .
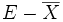
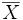
2. Si le point x de E n'est pas adhérent à X, il existe un voisinage de x qui ne rencontre pas X ; ce voisinage contient un ouvert U qui contient x et ne rencontre pas X. Il s'ensuit que le complémentaire de U dans E est un fermé qui contient X, et donc qui contient . Puisque x est dans U, x n'est pas dans .

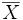
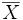
Intuitivement, l'adhérence d'une partie X contient tous les points de l'espace qui sont dans X ou qui sont trop près de X pour que l'on puisse y " bricoler " localement sans toucher à X.

Dans un espace métrique (la topologie est issue d'une distance sur l'espace considéré), l'adhérence d'un ensemble X est l'ensemble contenant toutes les limites de suites formée des éléments de X.

Exemples

L'ensemble des réels est l'adhérence de l'ensemble des rationnels . En effet, tout ouvert contenant un irrationnel contient un rationnel. Tout irrationnel est donc dans l'adhérence de .

L'adhérence d'un intervalle de , c'est l'intervalle fermé de mêmes bornes.

Densité

On dit qu'une partie X d'un espace topologique E est dense lorsque son adhérence est l'espace E tout entier. Une telle partie se caractérise donc par le fait que tout ouvert non vide en contient un point.

Un point x de X est dense si {x} est dense. On l'appelle parfois aussi point générique.

Intuitivement, les parties denses d'un espace sont donc des parties qui sont très grosses : on ne peut pas les éviter.

Pièges

Boules ouvertes et boules fermées

Celui qui n'est jamais tombé dans celui-ci, n'a jamais fait de topologie ! Dans un espace métrique, on définit des boules ouvertes et des boules fermées, et la tentation est grande d'utiliser dans ce cadre. Il est vrai que dans un certain nombre de cas, cela marche bien, notamment les avec la distance usuelle, et plus généralement pour la distance dans un espace vectoriel normé...

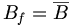
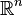
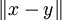
Néanmoins, c'est faux en général ; voyons l'exemple le plus simple : soit un ensemble E, avec au moins deux éléments. On définit une métrique dessus ainsi : la distance entre deux points distincts est 1. La boule ouverte de rayon 1 centrée en un point est donc ce point. La boule fermée de rayon 1 centrée en un point est donc l'espace entier. L'adhérence de la boule ouverte de rayon 1 centrée en un point est le point !

Un point c'est petit

Un point, ça n'a l'air de rien, et pourtant, dans certains espaces, certains points peuvent prendre une grande place !

Considérons l'ensemble des nombres premiers, auxquels on rajoute 0. On définit une topologie (via des fermés) de la façon suivante :

• un ensemble fini de nombre premiers est fermé ;
• l'espace entier est fermé ;

dans ce cas, l'adhérence de 0 est l'espace tout entier, ce qui signifie qu'on ne peut pas le mettre de côté pour travailler au voisinage d'un autre point. C'est un point dense/générique. (NB: en géométrie algébrique, ce genre de situation est très courant, car l'espace de base, le spectre d'anneau, vérifie souvent ce genre de propriétés ; en fait, cet exemple est )