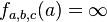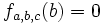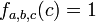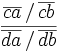Géométrie projective - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs est disponible ici.

La géométrie projective est le domaine des mathématiques qui modélise les notions intuitives de perspective et d'horizon. Elle étudie les propriétés des figures inchangées par projection.

Considérations historiques

La géométrie projective trouve ses origines dans le travail de Pappus (III^e avant Jésus-Christ) qui introduit le rapport anharmonique et fait référence à un travail d'Apollonius de Perga.

Elle a ensuite été étudiée au XVII^e siècle par des mathématiciens comme Pascal ou Desargues, avant de tomber dans l'oubli. C'est Poncelet dans son traité des propriétés géométriques des figures qui lui donne son véritable essor dans les débuts du XIX° siècle, en partant de considérations de géométrie pure. En effet la géométrie affine n'aurait pas permis cette découverte puisqu'elle interdisait l'intersection des droites parallèles, notion essentielle en géométrie projective.

Par suite la géométrie pure va fortement prédominer pendant tout le XIX° siècle jusqu'à ce que des méthodes analytiques soient enfin découvertes par August Ferdinand Möbius et Julius Plücker. Mais c'est Felix Klein qui, à la fin du XIX^e siècle, clarifie le lien entre géométrie projective et géométrie euclidienne.

C'est aussi à la même époque qu'eût lieu une évolution conceptuelle majeure ; auparavant la géométrie était la science des figures, les géomètres du tournant du siècle se concentrèrent sur les transformations desdites figures, les lois de composition internes des diverses transformations, la structure de certains groupes de transformations (questions de la commutativité, de l'associativité, de la transformation inverse, etc.), les invariants de telle ou telle famille de transformations, les axiomes minimaux permettant ces propriétés de transformations. Elle est aujourd'hui largement utilisée par les systèmes de vision par ordinateur et de rendu graphique (OpenGL).

Aperçu élémentaire

Pour ceux qui ne désirent qu'un aperçu élémentaire de ce qu'est la Géométrie Projective par rapport à la Géométrie Euclidienne ordinaire on peut dire que la Géométrie Projective est la science des figures qui ne se tracent qu'avec la règle seule alors que la géométrie euclidienne est en quelque sorte la science des figures qui se tracent à la règle et au compas.

La Géométrie Projective ignore les droites parallèles, les droites perpendiculaires, les isométries, les cercles, les triangles rectangles, isocèles , équilatéraux, etc. Dans sa définition elle comporte moins d'axiomes que la géométrie euclidienne et par suite elle est plus générale.

Enfin elle est remarquable par le fait qu'il est possible de poser certaines conventions de langage ( par exemple appeler parallèles deux droites qui se coupent sur une droite choisie du plan) qui permettent par la géométrie projective de retrouver les résultats de la Géométrie Euclidienne. ( Voir ci dessous le lien géométrie projective > géométrie euclidienne)

Espace projectif

Voir article détaillé : Espace projectif.

Un espace projectif est défini en mathématiques comme l'ensemble des droites vectorielles d'un espace vectoriel ; on peut imaginer l'œil d'un observateur placé sur l'origine d'un espace vectoriel, et chaque élément de l'espace projectif correspond à une direction de son regard.

Un espace projectif se démarque d'un espace vectoriel par son homogénéité : on ne peut distinguer en son sein aucun point particulier comme l'origine d'un espace vectoriel. En cela il se rapproche d'un espace affine.

Définition vectorielle

Soit $E \,\!$ un K-espace vectoriel (K est un corps, en général $\R \,\!$ ou $\mathbb{C} \,\!$ ), non réduit à ${0}$ . On définit sur $E - \{0\} \,\!$ la relation d'équivalence suivante :

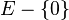
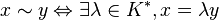
$x \sim y \Leftrightarrow \exists \lambda \in K^*, x=\lambda y \,\!$ .

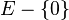
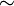
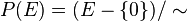
Alors on appelle espace projectif sur $E \,\!$ l'ensemble quotient de $E - \{0\} \,\!$ par la relation d'équivalence $\sim \,\!$ : $P(E) = (E - \{0\}) / \sim \,\!$ .

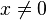
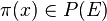
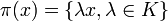
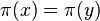
Pour chaque élément $x \neq 0 \,\!$ de $E \,\!$ on notera $\pi(x) \in P(E) \,\!$ sa classe d'équivalence : $\pi(x) = \{ \lambda x , \lambda \in K \} \,\!$ . On a donc : $\pi(x) = \pi(y) \,\!$ si et seulement si $x \,\!$ et $y \,\!$ sont colinéaires.

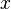
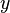
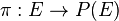
L'application $\pi : E \rightarrow P(E)\,\!$ est appelée projection canonique.

Plus simplement l'espace projectif $P(E) \,\!$ est l'ensemble des droites vectorielles de $E \,\!$ ; l'élément $\pi(x) \,\!$ de l'espace projectif est la droite vectorielle de $E \,\!$ dont un vecteur directeur est $x \,\!$ .

Si $E \,\!$ est de dimension finie $n \,\!$ alors on dit que $P(E) \,\!$ est de dimension finie et on note $n-1=dim \, P(E) \,\!$ la dimension de l'espace projectif. En particulier :

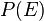
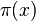
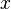
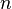
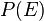
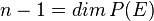
Si n=1 alors $P(E) \,\!$ est un singleton (dimension nulle) ;
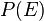
Si n=2 alors $E \,\!$ est un plan vectoriel et $P(E) \,\!$ est appelé droite projective.
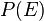
Si n=3 alors $P(E) \,\!$ est appelé plan projectif ; c'est le cadre le plus courant pour faire de la géométrie.

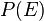
Si l'espace $E \,\!$ est l'espace vectoriel de dimension $n \,\!$ " typique ", c'est-à-dire $K^n \,\!$ alors on a une notation particulière pour l'espace projectif : $P^{n-1}(K) \,\!$ au lieu de $P(K^n) \,\!$ .

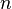
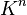
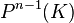
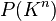
Définition affine

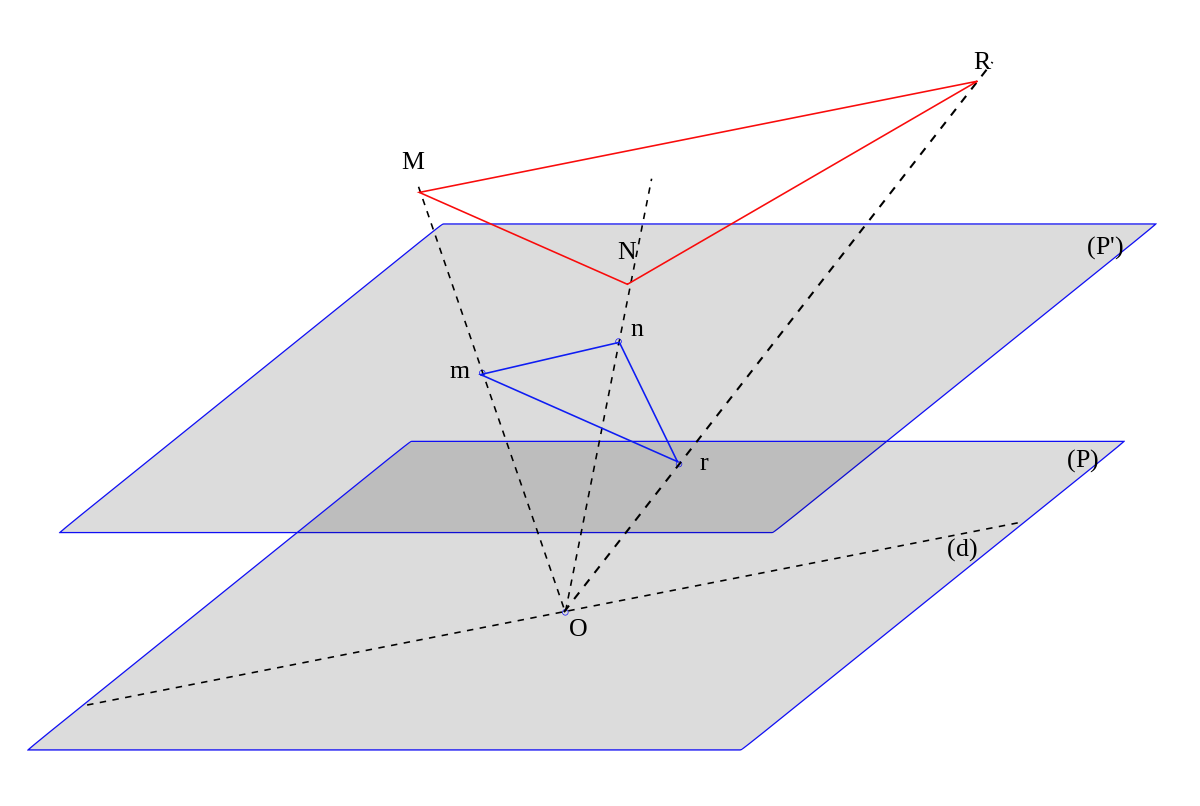
Espace projeté dans un plan projectif

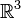
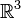
Cette définition très formelle d'un espace projectif ne doit pas faire oublier que cette notion est née de la projection centrale et est, avant tout, une notion géométrique. Pour prendre l'exemple de l'espace projectif de $\mathbb{R}^3$ , on peut observer le dessin ci-contre où les points $m$ , $n$ et $r$ appartiennent au plan $(P')$ . Il faut imaginer un observateur placé en $O$ . Cet observateur voit tous les points de la droite $(O M)$ en $m$ , ceux de la droite $(O R)$ en $r$ et ceux de la droite $(O N)$ en $n$ . les droites $(d)$ du plan $(P)$ ne sont pas vues comme des points de $(P')$ . Il y a donc bijection entre les droites vectorielles de $\mathbb{R}^3$ non parallèles à $(P)$ et les points du plan $(P')$ .

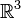
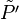
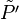
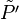
L'espace projectif de $\mathbb{R}^3$ est donc en bijection avec le plan affine $(P')$ auquel on ajoute l'ensemble des droites vectorielles de $(P)$ . Un plan projectif $\tilde{P'}$ est donc constitué d'un plan affine $(P')$ qui contient l'ensemble des points propres de $\tilde{P'}$ auquel on adjoint toutes les droites vectorielles (ou directions) de $(P')$ . Chaque point du deuxième ensemble s'appelle point impropre de $\tilde{P'}$ ou point à l'infini.

Cette notion permet, par exemple, de parler, dans un plan, d'intersection entre deux droites quelconques : les droites seront sécantes en un point propre de $(P')$ ou bien en un point impropre dans le cas où les droites sont parallèles.

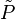
Cette notion se généralise à tout espace projectif $\tilde P$ de dimension $n$ : c'est un espace affine $(P)$ de dimension $n$ auquel on adjoint l'ensemble des directions de $(P)$ .

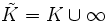
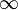
En particulier, si $(P)$ = $K$ , la droite projective associée est l'ensemble $\tilde{K} = K \cup {\infty} \,\!$ où $\infty$ est un point extérieur à $K \,\!$ , prolongeant les opérations algébriques de la manière suivante :

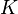
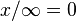
pour tout $x$ de $K$ , $x/\infty =0$
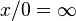
pour tout $x$ de $K *$ , $x/0 =\infty$

Cette double relation, d'une part avec un espace vectoriel quotienté, d'autre part avec un espace affine complété fait la richesse de l'étude de la géométrie projective. De même, ce double aspect sera important à conserver quand il s'agira de donner des coordonnées aux points de l'espace projectif.

Repérage

Coordonnées homogènes

Voir article détaillé : coordonnées homogènes.

Dans un espace projectif de dimension $n$ , donc associé à un espace vectoriel de dimension $n + 1$ , chaque point $m$ de $P (E)$ est associé à une famille de vecteurs de $E$ tous colinéaires. Si $E$ est muni d'une base canonique, on appelle coordonnées homogènes du point $m$ , les coordonnées d'un vecteur quelconque $x$ tels que $\pi(x) = m\,$ . Un point possède donc une famille de coordonnées toutes proportionnelles entre elles. 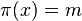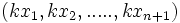Autrement dit, si $(x_1, x_2, ....., x_{n+1})\,$ est un système de coordonnées homogènes de $m$ , il en est de même de $(kx_1, kx_2, ....., kx_{n+1})\,$ pour tout élément $k$ non nul de $K$ .

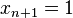
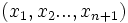
Parmi toutes ces coordonnées, il arrive souvent que l'on en privilégie une pour retrouver un espace affine de dimension $n$ . Parmi tous les représentants de $m$ , on privilégie celui dont la dernière coordonnée, par exemple, vaut $1$ . Cela revient à dire que l'on a projeté l'espace dans l'hyperplan d'équation $x_{n+1} = 1\,$ . 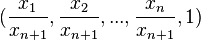Si $(x_1, x_2 ..., x_{n+1})\,$ est un système de coordonnées de $m$ , on privilégie le système de coordonnées $({x_1\over x_{n+1}}, {x_2 \over x_{n+1}}, ..., {x_n \over x_{n+1}} , 1)\,$ . Cela ne vaut évidemment que si $m$ est un point propre de $P (E)$ .

Les points impropres sont représentés par des systèmes de coordonnées homogènes dont la dernière coordonnée est nulle.

On remarque alors bien là la correspondance entre

les point propres de $P (E)$ et les points d'un espace affine de dimension $n$
les points impropres de $P (E)$ et les directions d'un espace vectoriel de dimension $n$

Choisir arbitrairement de mettre une coordonnée à $1$ dans les coordonnées homogènes permet de définir des cartes différentes.

Repère d'un espace projectif

Voir l'article détaillé: Repère projectif.

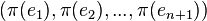
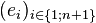
Un espace vectoriel de dimension n se repère par une base de n vecteurs indépendants. Un espace affine de dimension n se repère à l'aide de n + 1 points non liés. Un espace projectif de dimension n se repère à l'aide de n+2 points. On pourrait penser que n+1 points seraient suffisants en prenant par exemple $(\pi(e_1), \pi(e_2),...,\pi(e_{n+1}))\,$ où $(e_i)_{i \in \{1 ; n+1\}}$ forme une base de l'espace vectoriel de dimension n+1 associé à l'espace projectif. 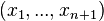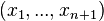Les coordonnées d'un point m dans ce repère seraient alors $(x_1, ..., x_{n+1}) \,$ où $(x_1, ..., x_{n+1})\,$ sont les coordonnées de x tels que $\pi(x)= m\,$ mais il faudrait que ces coordonnées soient indépendantes du représentant choisi pour les vecteurs de la base : $\pi(e_1)\,$ , par exemple, a un autre représentant qui est $2e_1\,$ . 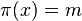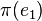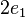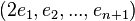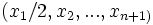Et dans la base $(2e_1, e_2, ..., e_{n+1})\,$ x n'a pas le même système de coordonnées $(x_1/2, x_2, ..., x_{n+1)}\,$ .

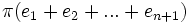
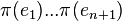
Il faut donc empêcher cette ambiguïté et limiter le choix d'autres représentants des vecteurs de base à des vecteurs colinéaires aux précédents mais de même coefficient de colinéarité. Il suffit pour cela de définir un n+2 ième point correspondant à $\pi(e_1 + e_2 + ...+ e_{n+1})\,$ . 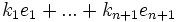Ainsi, si on choisit d'autres représentants de $\pi(e_1) ...\pi(e_{n+1})\,$ avec des coefficients de colinéarité différents, le vecteur $k_1e_1 + ... 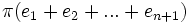+ k_{n+1}e_{n+1}\,$ ne sera plus un représentant de $\pi(e_1 + e_2 + ...+ e_{n+1})\,$ .

Sous-espace projectif

Voir l'article détaillé : Sous-espace projectif.

Comme il existe des sous-espaces vectoriels d'espace vectoriel ainsi que des sous-espaces affine d'espace affine, il existe de même des sous-espaces projectifs d'espace projectif. Ils sont constitués des projetés des sous-espaces vectoriels de l'espace vectoriel associé. On parlera donc de droite projective dans un plan projectif, de plan projectif dans un espace projectif. La règle des dimensions et l'existence de points à l'infini permettent de simplifier les règles d'incidence.

Birapport sur une droite projective

Voir article détaillé : rapport anharmonique.

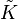
Si a, b, c et d sont 4 points (a,b et c distincts) d'une droite projective D, il existe un unique isomorphisme de D sur $\tilde K$ , $f a, b, c$ tel que

$f_{a, b, c}(a) = \infty$
$f_{a, b, c}(b) = 0\,$
$f_{a, b, c}(c) = 1\,$

On appelle birapport de a, b, c, d, noté [a:b:c:d] la valeur de $f a, b, c (d)$ .

Si a, b, c et d sont 4 points propres distincts de D, on retrouve la définition ancienne du birapport ou rapport anharmonique :

Transformation projective ou homographie

Voir l'article : Application projective.

Les transformations projectives ou homographies sont des transformations étudiées en géométrie projective. Elles s'obtiennent comme composée d'un nombre fini de projections centrales. Elles décrivent ce qui arrive aux positions observées de différents objets quand l'œil de l'observateur change de place. Les transformations projectives ne conservent par toujours les distances ni les angles mais conserve les propriétés d'incidence et le birapport - deux propriétés importantes en géométrie projective. On trouve des transformations projectives sur des droites, dans des plans et dans l'espace.

Propriété fondamentale : En dimension finie, une transformation projective est entièrement déterminée par l'image d'un repère de l'espace projectif.

Définition analytique d'une homographie

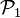
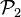
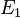
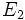
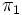
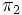
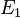
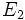
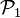
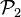
Soient 2 espaces projectifs $\mathcal P_1$ et $\mathcal P_2$ associés respectivement aux espaces vectoriels $\quad E_1$ et $\quad E_2$ . On désigne par $\quad \pi_1$ et $\quad \pi_2$ les projections canoniques de $\quad E_1$ (resp. $\quad E_2$ ) sur $\mathcal P_1$ (resp. $\mathcal P_2$ ).

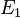
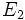
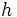
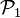
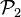
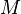
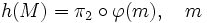
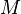
On peut alors effectuer un " passage au quotient " des applications linéaires injectives de $\quad E_1$ dans $\quad E_2$ . Une telle application linéaire $\quad \varphi$ étant donné on peut définir une application $\quad h$ de $\mathcal P_1$ dans $\mathcal P_2$ transformant le point $\quad M$ en $h(M)=\pi_2 \circ \varphi (m),\quad m$ désignant un représentant de $\quad M$ . 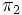Naturellement pour que cette définition soit cohérente, nous devons vérifier qu'elle ne dépend pas du représentant choisi, ce qui est immédiat vu la linéarité de $\varphi$ et la définition de $\quad \pi_2$ .

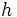
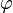
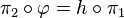
L'application $\quad h$ est l'homographie associée à $\quad \varphi$ . Elle est de façon plus concise définie par l'égalité: $\pi_2 \circ \varphi = h \circ \pi_1$ .

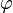
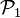
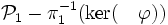
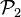
On peut aussi parler plus généralement d'application projective, en n'exigeant pas l'injectivité de l'application linéaire $\quad \varphi$ initiale ; le même procédé de passage au quotient fournira une application définie seulement sur une partie de $\mathcal P_1$ : $\mathcal P_1-\pi_1^{-1}(\ker(\quad \varphi))$ , et à valeurs dans $\mathcal P_2$ . On ne parlera pas alors d'homographie.

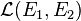
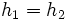
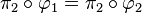
Il existe une infinité d'applications linéaires associées à une homographie mais ces applications linéaires forment une droite vectorielle de $\mathcal L(E_1,E_2)$ puisque $\quad h_1=h_2$ entraîne $\pi_2 \circ \varphi _1=\pi_2 \circ \varphi _2$ .

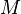
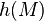
En dimensions finies p,n, si on dispose d'un système de coordonnées homogènes, une homographie pourra être définie par une classe de matrices non nulles de format (n+1)*(p+1) toutes multiples de l'une d'elles. A étant une de ces matrices et X une matrice-colonnes de coordonnées homogènes de $\quad M$ , AX sera matrice colonne de coordonnées homogènes de $\quad h(M)$ (tout ceci étant donc défini à un facteur près).

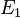
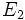
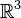
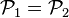
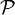
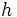
Exemple et discussion (géométrie plane).: Nous prenons pour $\quad E_1$ et $\quad E_2$ l'espace $\mathbb R^3$ . $\mathcal P_1 = \mathcal P_2$ est le plan projectif $\mathcal P$ . Envisageons une homographie $\quad h$ définie par la matrice 3*3 A que nous supposons diagonalisable. 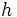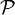On peut donc calculer les coordonnées homogènes des transformés de tout point.; Les 3 directions propres sont indépendantes et définissent 3 points invariants par $\quad h$ de $\mathcal P$ . Ces 3 points ont respectivement comme matrices-colonne de coordonnées homogènes $X 1, X 2, X 3$ (vecteurs propres de la matrice, à un facteur non nul près).; Inversement la connaissance de ces 3 points invariants détermine-t-elle l'homographie, c'est-à-dire A, à un facteur près ? Pour cela il faudrait pouvoir calculer les valeurs propres de A (à un facteur de proportionnalité près toujours). 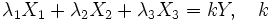Or on n'a évidemment aucun moyen pour cela en ne connaissant que les directions propres.; Par contre si on se donne par exemple le transformé du point de coordonnées homogènes $X 1 + X 2 + X 3$ en le point de coordonnées homogènes $Y$ , on aura en désignant par $λ 1,λ 2,λ 3$ les valeurs propres de A: $\lambda_1X_1+\lambda_2X_2+\lambda_3X_3=kY,\quad k$ quelconque non nul, ce qui permet bien de calculer en résolvant le système les valeurs propres à un coefficient de proportionnalité près.; Les 4 points (les 3 points invariants plus le 4^e défini ci-dessus) définissent un repère projectif (voir plus haut) et la connaissance de la transformation de ce repère projectif détermine entièrement l'homographie.

Exemple d'homographie: Les transformations par polaires réciproques.

Topologie

Voir l'article détaillé : Topologie en géométrie projective.

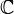
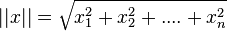
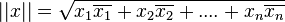
Si E est un espace vectoriel sur $\mathbb R$ ou $\mathbb C$ de dimension finie, on peut définir sur E une topologie issue de la distance induite par la norme $||x|| = \sqrt{x_1^2 + x_2^2 + .... + x_n^2}$ dans le cas réel et $||x|| = \sqrt{x_1\overline{x_1} + x_2\overline{x_2} + .... + x_n\overline{x_n}}$ dans le cas complexe.

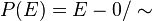
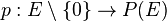
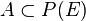
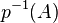
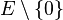
Cette topologie permet de définir sur l'espace quotient $P(E)=E-{0}/\sim$ une topologie, dite topologie quotient. Si $p:E\setminus\{0\}\rightarrow P(E)$ désigne l'application de passage au quotient, on dira qu'une partie $A\subset P(E)\,$ est ouverte si son image réciproque $p^{-1}(A)\,$ est ouverte dans $E\setminus\{0\}\,$ . On vérifie que l'on définit bien ainsi un espace topologique

On montre que $P(E)\,$ est compact.

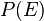
On munira donc l'espace projectif P(E) de cette topologie. Elle permet de parler d'homéomorphisme et de remarquer, par exemple, que la droite projective réelle est homéomorphe à un cercle, la droite projective complexe étant homéomorphe à une sphère (voir l'article sphère de Riemann pour un homéomorphisme explicite).

Dualité

Voir l'article détaillé : Dualité (géométrie projective).

Si E est un K-espace vectoriel de dimension finie n, son dual E* est aussi un K-espace vectoriel de dimension n. On peut donc associer à l'espace projectif P(E), son dual P(E*). Une droite de P(E*) correspondra à un faisceau d'hyperplans dans P(E). Le passage au dual permet d'inverser un grand nombre de propriétés géométriques.

À quoi sert la géométrie projective ?

La géométrie projective a permis de simplifier grandement des théorèmes de géométrie plane comme le théorème de Pappus ou le théorème de Desargues.
Muni d'une topologie, l'espace projectif est le point de départ de l'étude de la géométrie différentielle.
Enfin, avec le développement de la représentation en 2D d'objets en 3D, la géométrie projective a montré la puissance des outils de dessin assisté par ordinateur qui ont été mis en place.
Si l'espace projectif, comparé à l'espace usuel, c'est-à-dire l'espace affine, peut sembler être un objet plus compliqué, il est indéniable que pour de nombreuses situations, l'espace projectif est le bon cadre pour travailler. Pour donner un exemple, si $C$ et $C'$ sont deux courbes planes (complexes) de degré respectif $d$ et $d'$ alors, si on voit ces courbes comme des sous-variétés du plan affine, le théorème de Bezout dit que le nombre de points d'intersection entre $C$ et $C'$ est toujours inférieur ou égal à $d d'$ . En revanche, si on voit ces courbes comme des sous-variétés du plan projectif, alors le théorème dit que le nombre de points d'intersection (comptés avec multiplicité) est égal à $d d'$ . Il y a de nombreuses autres situations où les théorèmes s'énoncent sous un forme plus belle en géométrie projective.
En sus des aspects utilitaires, on peut insister sur la gymnastique intellectuelle et sur le sentiment de perfection esthétique que procurent certains théorèmes et certains axiomes de plans projectifs.

Bibliographie

Michèle Audin, Geometry, Universitext, Springer, ISBN-13: 978-3540434986
Marcel Berger, Géométrie [détail des éditions] (Tome 1)
De la Géométrie Projective à la Géométrie Euclidienne L'Hexagramme Mystique de Pascal
Petite encyclopédie de mathématique (Ed. Didier)
Méthodes modernes en géométrie de Jean Fresnel
D. Lehmann et R. Bkouche, Initiation à la géométrie, PUF 1988, ISBN 2 13 040160 0
J.-C. Sidler, Géométrie projective, InterEditions 1993

Articles de géométrie
Géométrie - Géométrie affine - Géométrie euclidienne - Géométrie projective - Géométrie hyperbolique - Géométrie non euclidienne - Géométrie synthétique - Programme d'Erlangen - Géométrie du XXe siècle - Topologie différentielle - Topologie algébrique - Géométrie différentielle - Géométrie riemannienne - Géométrie symplectique - Géométrie algébrique
Accéder au portail de la géométrie

Le trou noir supermassif Ansky vient de se réveiller ⚫

Voici ce qui rend notre cerveau vraiment unique 🧠

Asymétrie matière-antimatière: une nouvelle pièce du puzzle dévoilée 🧩

Neige en inuit, goût en japonais... comment les langues décomposent la réalité ? 💬

La physique révèle les secrets d'un strike parfait au bowling 🎳

Le TDAH associé à la démence 🧠

Découverte d'une nouvelle forme d'intrication quantique, une première en 20 ans ⚛️

Le régime cétogène montre des surprises sur le cholestérol 🧐

Un tango observationnel révèle une Super-Terre 🔭

Cette expérience montre que la graisse brune augmente fortement la longévité 🕒

L'Univers comme jamais vu auparavant: les révélations du fond diffus cosmologique 🔭

C'est sérieux: de la bave pourrait révolutionner la conception de bioplastiques 🪱

Découverte: le trou noir central de notre galaxie pourrait anéantir la vie sur Terre 💥

Etude scientifique: ces aliments nous font vieillir 🍽️

Pourquoi notre visage est-il plus petit et délicat que celui des Néandertaliens ? 🤔

A 18 ans, il découvre 1,5 million d'objets célestes inconnus avec son algorithme d'IA 🌟

Que sont ces objets rouges et aplatis, qualifiés d'UFOs par les astronomes ? 🔭

Une méthode simple pour améliorer les performances en mathématiques 🧮

Que sont ces étranges éclairs rouges photographiés au-dessus de l'Himalaya ? ⚡

Nous descendons non pas d'un, mais d'au moins deux groupes anciens 🧬

Un nuage géant de 160 000 soleils découvert dans notre Voie lactée 🔭

Connaissez-vous le rat-kangourou musqué, ce marsupial à la démarche unique ? 🦘

Comment une poignée de traders a fait s'effondrer deux cryptomonnaies 📉

Première cartographie titanesque d'un cerveau, avec 500 millions de connexions neuronales 🧠

Cette double supernovae proche est inexorable, voici la date... qui va vous surprendre 💥

Un océan phosphorescent: comment s'explique ce phénomène rare et féerique ? 🌊

L'ELT pourrait-il découvrir une vie extraterrestre dès 2028 ? 🔭

Cet édulcorant tue les superbactéries résistantes 🍬

Les neutrinos, la clé de la gravité quantique ? 👀

En Italie, les éruptions explosives de ce volcan déjouent les pronostics 🌋

Que sont ces spaghettis au cœur de notre galaxie ? 🔭

Des scientifiques ont créé une "bombe intelligente" contre le cancer 🎯

Les nanoplastiques, l'amiante du 21ème siècle ? 🔬

Compétition cellulaire: des forces sculptent nos tissus 🛠️

Le climat en Europe et au États-Unis pourrait changer bien plus radicalement que supposé 🌍

Découverte: ce dinosaure avait des poches d'air dans les os 🦴

La vie sur Titan, si elle existe, ressemblerait à quoi ? 🪐

Magnétisme et biologie s'allient contre le cancer 🧲

WR 104: on en sait plus sur cette "étoile de la mort" qui menace la Terre ☄️

Découverte: des bactéries respiraient de l'oxygène 1 milliard d'années avant la Grande Oxydation 🫧

Découverte d'un nouveau type de vent solaire rapide ☀️

Les dinosaures n'étaient pas en déclin avant l'astéroïde 🦖

Ce robot-cheval est véritablement tout-terrain 🐎

Comment un mauvais sommeil peut endommager votre cerveau ? 🧠

Découverte de microbes cachés qui purifient l'eau sans que nous le sachions 💧

Bonne nouvelle pour les enfants de la Lune 🌙

Du CO2 détecté dans l'atmosphère d'une exoplanète proche 🔭

Le café et le thé impactent le cancer, mais dans quel sens ? ☕

Une IA révèle des bulles cosmiques dans notre galaxie 🫧

Lorsque l'alcool stimule ses phéromones sexuelles et rend plus séduisant 🍷

Page générée en 0.184 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise