Espace de Banach - Définition

Un espace de Banach est un espace vectoriel normé complet pour la distance issue de sa norme. Comme la topologie déduite de sa distance est compatible avec sa structure d’espace vectoriel, c’est un espace vectoriel topologique. Les espaces de Banach possèdent de nombreuses propriétés qui font d'eux un outil essentiel pour l'analyse fonctionnelle.

Propriété des fermés emboîtés

Soit une suite décroissante de fermés non vides d'un espace de Banach telles que le diamètre de chaque fermé soit réel et que la suite des diamètres tende vers 0. Alors l'intersection des fermés est réduite à un singleton.

Cette propriété permet de démontrer qu'un espace de Banach est de Baire.

Noter que cette propriété peut être fausse sans l'hypothèse que les diamètres tendent vers 0, même si on suppose les fermés bornés.

Théorème de Banach-Steinhaus

Voir l'article de fond : Théorème de Banach-Steinhaus.

Soient E un espace de Banach, et F un espace vectoriel normé. Soit une famille d'éléments de (voir application linéaire) et soit A l'ensemble des vecteurs tels que . Alors soit A est maigre, c'est-à-dire réunion dénombrable d'ensembles rares (un ensemble est rare si l'intérieur de son adhérence est vide) et son complémentaire est dense, soit . En particulier, si A = E, seule la seconde éventualité est possible.

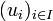
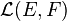
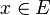
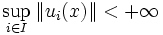
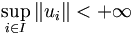
Remarque : la dernière norme utilisée est la norme d'opérateur (ou norme subordonnée).

Littérature

• Stefan Banach : Théorie des opérations linéaires. -- Warszawa 1932. (Monografie Matematyczne; 1) Zbl 0005.20901