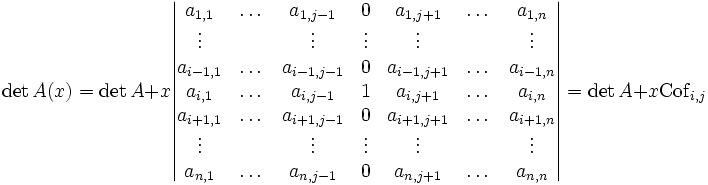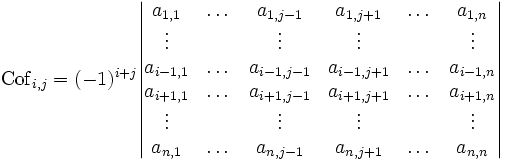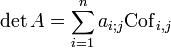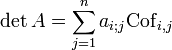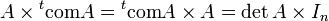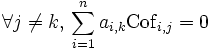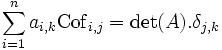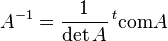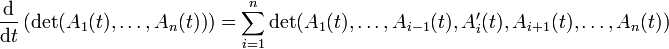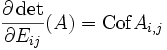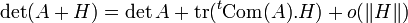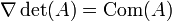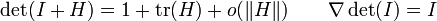Comatrice - Définition
En algèbre linéaire, la comatrice d'une matrice carrée A est une matrice introduite par une généralisation du calcul de l'inverse de A. Elle a une importance considérable pour l'étude des déterminants. Ses coefficients sont appelés cofacteurs de A, et ils permettent d'étudier les variations de la fonction déterminant.
La comatrice est aussi appelée matrice des cofacteurs, ou encore, hélas, matrice adjointe (par exemple dans le logiciel Maple).
Matrice ayant un coefficient variable
Le déterminant pour les matrices est naturellement défini comme une fonction sur les n vecteurs colonnes de la matrice. Il est cependant légitime de le considérer aussi comme une fonction qui aux n2 coefficients de la matrice associe un scalaire.
Quand on gèle tous les coefficients de la matrice à l'exception d'un seul, le déterminant est une fonction affine du coefficient variable. L'expression de cette fonction affine est simple à obtenir comme cas particulier de la propriété de n-linéarité ; elle fait intervenir un déterminant de taille n-1, appelé cofacteur du coefficient variable.
Ces considérations permettent d'établir une formule de récurrence ramenant le calcul d'un déterminant de taille n, à celui de n déterminants de taille n-1 : c'est la formule de Laplace.
Cofacteur
Soit A une matrice carrée de taille n. On observe l'effet d'une modification d'un des coefficients de la matrice, toutes choses égales par ailleurs. Pour cela on choisit donc deux indices i pour la ligne et j pour la colonne, et on note A(x) la matrice dont les coefficients sont les mêmes que ceux de A, sauf le terme d'indice i,j qui vaut ai,j+x. On écrit la formule de linéarité pour la j-ème colonne
Le déterminant noté Cofi,j est appelé cofacteur d'indice i,j de la matrice A. Il admet les interprétations suivantes
- augmenter de x le coefficient d'indice i,j de la matrice (toutes choses égales par ailleurs) revient à augmenter le déterminant de x fois le cofacteur correspondant
- le cofacteur est la dérivée du déterminant de la matrice A(x)
Dans la pratique, on calcule les cofacteurs de la façon suivante : on appelle M(i;j) le déterminant de la sous-matrice déduite de M en ayant enlevé la ligne i et la colonne j (on parle de mineur pour un tel déterminant). Alors le cofacteur est (-1)i+j fois M(i;j).
Formules de Laplace
Si n>1 et A est une matrice carrée de taille n alors on peut calculer son déterminant en fonction des coefficients d'une seule colonne et des cofacteurs correspondants. Cette formule, dite formule de Laplace, permet ainsi de ramener le calcul du déterminant à n calculs de déterminants de taille n-1.
- Formule de développement par rapport à la colonne j
- On peut donner également une formule de développement par rapport à la ligne i
Quitte à transposer la matrice, il suffit de prouver la formule du développement par rapport à une colonne.
On considère la matrice M0 obtenue en remplaçant la colonne j de la matrice A par une colonne de 0. Le déterminant de M0 est nul.
On passe de M0 à A en modifiant successivement les différents coefficients de la colonne j. On fait d'abord passer le premier coefficient de 0 à a1;j, puis le second de 0 à a2;j et ainsi de suite. La première opération revient à ajouter a1;j multiplié par son cofacteur, la seconde a1;j multiplié par son cofacteur.
Au bout du compte, pour passer du déterminant de M0 (nul) à celui de A, on a ajouté successivement tous les termes intervenant dans la formule de Laplace.
Remarque : pour la correction de la preuve, il est important de noter que les cofacteurs à chaque étape sont bien les mêmes que ceux de la matrice A, puisqu'on ne modifie que la colonne j.
Généralisation
On introduit la comatrice de A, matrice constituée des cofacteurs de A. On peut généraliser les formules de développement du déterminant par rapport aux lignes ou colonnes
On prend de nouveau pour matrice M0 la matrice obtenue en remplaçant la colonne j de la matrice A par une colonne de 0. Le déterminant de M0 est nul.
Mais cette fois au lieu de faire apparaître en colonne j les coefficients ai;j, on fait apparaître successivement les coefficients ai;k d'une autre colonne. La matrice finale obtenue admet alors deux colonnes identiques, donc est elle aussi de déterminant nul. Ceci signifie
En effet par rapport à la démonstration précédente, si les coefficients ont changé, les cofacteurs non.
Si on ajoute à cette étude le cas j=k qui a été examiné dans le paragraphe précédent, on arrive à
qui est exactement, composante par composante, la formule souhaitée.
La matrice transposée de la comatrice est appelée matrice complémentaire de A. Notamment si A est inversible, l'inverse de A est un multiple de la matrice complémentaire. Ce qui veut dire qu'on a obtenu une formule pour l'inverse, ne nécessitant que des calculs de déterminants
Cette formule est encore valable si les matrices sont à coefficients dans un anneau A. Elle est utilisée pour démontrer que M est inversible en tant que matrice à coefficients dans A si et seulement si det(M) est inversible comme élément de A.
Elle est d'un intérêt limité pour calculer explicitement des inverses de matrices; en pratique elle est trop lourde dès que n=4 et la méthode plus élémentaire à base d'opérations élémentaires sur les lignes (inversion par pivot de Gauss) est plus efficace, aussi bien pour l'homme que pour la machine.
Propriétés de la comatrice
Nous avons
- com(In) = In
et
- pour toutes matrices d'ordre n M et N, com(MN) = com(N) com(M)
La comatrice est aussi compatible avec la transposition :
- com(tM) = t (com(M)).
de plus,
- det(com(M)) = det(M)n-1.
Si p(t) = det(M - tIn) est le polynôme caractéristique de M et que q est le polynôme défini par q(t) = (p(0) - p(t))/t, alors
- tcom(M) = q(M).
La comatrice apparaît dans la formule de la dérivée d'un déterminant.
Pour
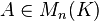
- si A est de rang n (i.e. A inversible), Com(A) aussi. On a alors
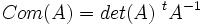
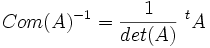
- si A est de rang n-1, Com(A) est de rang 1.
- si A est de rang au plus n-2, Com(A)=0.
Si
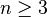
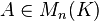
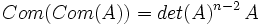
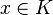
Si
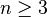
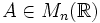
Variations de la fonction déterminant
Le formule de Leibniz montre que le déterminant d'une matrice A s'exprime comme somme et produit de composantes de A. Il n'est donc pas étonnant que le déterminant ait de bonnes propriétés de régularité. On suppose ici que K est le corps des réels.
Déterminant dépendant d'un paramètre
Si
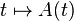
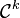
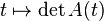
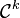
La formule de dérivation s'obtient en faisant intervenir les colonnes de A
Cette formule est analogue formellement à la dérivée d'un produit de n fonctions numériques.
Le déterminant comme fonction sur l'espace des matrices
- L'application qui à la matrice A associe son déterminant est continue.
Cette propriété a des conséquences topologiques intéressantes : ainsi le groupe GLn(


- Cette application est en fait différentiable, et même
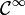
En effet le calcul des cofacteurs peut être vu précisément comme un calcul de dérivée partielle
Toutes ces dérivées partielles étant elles-mêmes des déterminants, par récurrence le déterminant est
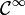
C'est-à-dire que si on munit Mn(

Notamment pour le cas où A est l'identité
| Articles de mathématiques en rapport avec l'algèbre linéaire |
| Espace vectoriel | Base | Dimension | Matrice | Application linéaire | Déterminant | Trace | Rang | Théorème des facteurs invariants | Réduction d'endomorphisme | Réduction de Jordan | Décomposition de Dunford | Valeur propre | Polynôme caractéristique | Forme linéaire | Espace dual | Orthogonalité | Produit scalaire | Produit vectoriel | Polynôme d'endomorphisme | Polynôme minimal | Tenseur | Pseudovecteur | Covecteur | Algèbre multilinéaire |