Bilinéaire - Définition
Définition
Soit E, F et G trois espaces vectoriels sur un corps

Soit
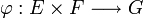

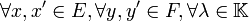
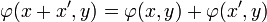
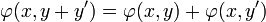
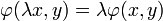
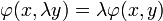
Si
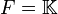
| Articles de mathématiques en rapport avec l'algèbre linéaire |
| Espace vectoriel | Base | Dimension | Matrice | Application linéaire | Déterminant | Trace | Rang | Théorème des facteurs invariants | Réduction d'endomorphisme | Réduction de Jordan | Décomposition de Dunford | Valeur propre | Polynôme caractéristique | Forme linéaire | Espace dual | Orthogonalité | Produit scalaire | Produit vectoriel | Polynôme d'endomorphisme | Polynôme minimal | Tenseur | Pseudovecteur | Covecteur | Algèbre multilinéaire |

















































