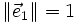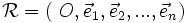Base orthonormale - Définition
Base orthonormale
Soit En un espace vectoriel euclidien de dimension n, où n est un entier naturel non nul, et
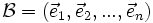
- Si n = 1, alors
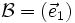
- Si n > 1, alors

-
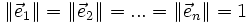
- et,
- pour tout
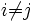
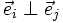
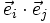
Le terme " base orthonormée " est parfois abrégé par le sigle BON.
Repère orthonormal
Soient An un espace affine euclidien associé à l'espace vectoriel euclidien En et O un point quelconque de An, alors le repère
est dit orthonormal si et seulement si sa base associée
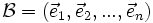
Le terme " repère orthonormé " est parfois abrégé par le sigle RON.
En géométrie dans l'espace
En géométrie dans l'espace, la base est en général notée
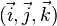
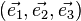
La base est dite " directe " si

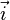
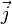
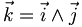
Le terme " base orthonormée directe " est parfois abrégé par le sigle BOD.
Si la base associèe à un repère est orthonormée directe, le repère est un repère orthonormé direct, terme parfois abrégé par le sigle ROND.
Voir l'article Orientation (mathématiques).