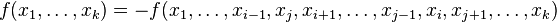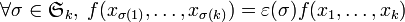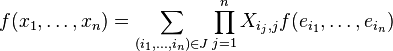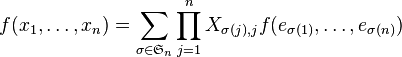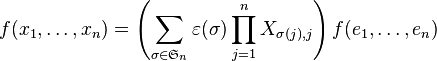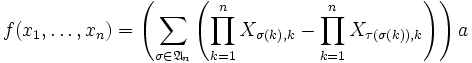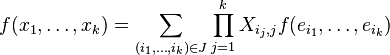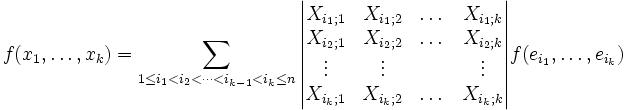Application multilinéaire - Définition
En algèbre linéaire, une application multilinéaire est une fonction mathématique à plusieurs variables vectorielles qui est linéaire en chaque variable.
Quelques exemples classiques :
- Le produit scalaire est une fonction bilinéaire symétrique à deux variables vectorielles, et qualifiée de forme bilinéaire car à valeur dans le corps de base
- Le déterminant est une fonction multilinéaire antisymétrique des colonnes (ou rangées) d'une matrice carrée.
L'étude systématique des applications multilinéaires permet d'obtenir une définition générale du déterminant, du produit extérieur et de nombreux autres outils ayant un contenu géométrique. La branche de l'algèbre correspondante est l'algèbre multilinéaire. Mais il y a également de très nombreuses applications dans le cadre des variétés, en topologie différentielle.
Forme k-linéaire
Soit k>1 un entier. Soit E un


Il ne faut pas confondre cette notion avec celle d'application linéaire de Ek dans

De façon informelle, il faut se représenter une application k-linéaire comme une application produit de k termes, avec une propriété de type distributivité.
Écriture en composantes
Si l'espace E est de dimension finie n et muni d'une base e1, ..., en, on peut décomposer chaque vecteur
Alors l'expression d'une forme k-linéaire sur le k-uplet x1, ..., xk devient
La connaissance des nk valeurs
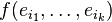
Les formes k-linéaires alternées (alternées ???) sur un espace vectoriel E de dimension n forment donc un espace vectoriel Lk(E), de dimension nk.
Forme k-linéaire alternée
Une forme k-linéaire sur E est dite alternée si elle s'annule à chaque fois qu'on l'évalue sur un k-uplet contenant deux vecteurs identiques
Antisymétrie
Toute forme k-linéaire alternée est antisymétrique, c'est-à-dire que l'échange de deux vecteurs a pour effet de changer le résultat obtenu en son opposé
Sauf dans le cas où

On peut se contenter de travailler avec deux variables, en fixant toutes les autres. On fait donc la preuve dans le cas d'une forme bilinéaire f sur E.
Si f est alternée, alors pour deux vecteurs x et y de E,
- f(x + y,x + y) = 0 = f(x,x) + f(x,y) + f(y,x) + f(y,y) = f(x,y) + f(y,x)
ce qui montre que f(x,y) et f(y,x) sont opposés. Donc f est antisymétrique.
Si f est antisymétrique, pour tout x f(x,x) est un scalaire, égal à son opposé. Si la caractéristique de

Forme plus générale de la propriété d'antisymétrie
Si f est une forme k-linéaire antisymétrique, on peut effectuer plusieurs échanges de vecteurs successifs. On réalise ainsi une permutation des vecteurs, obtenue comme une succession de transpositions. À chaque étape, le signe est changé en son opposé. Finalement l'effet d'une permutation générale des vecteurs est la multiplication de la valeur obtenue par la signature de la permutation.
Cette propriété s'applique notamment pour les formes k-linéaires alternées.
Forme n-linéaire alternée en dimension n
Dans cette section on étudie le cas particulier k=n qui permet de construire le déterminant.
Si l'espace E est de dimension finie n et muni d'une base e1, ..., en, on peut décomposer chaque vecteur
Alors l'expression d'une forme n-linéaire alternée sur le n-uplet x1, ..., xn se simplifie. Après suppression des termes où figurent deux fois le même vecteur, il vient
où J est l'ensemble des n-uplets

Mais alors

Enfin par antisymétrie
Ainsi la connaissance d'un seul scalaire,

L'ensemble An(E) des formes n-linéaires alternées sur un espace vectoriel de dimension n constitue un espace vectoriel de dimension 1.
L'application
est linéaire. On vient de montrer qu'elle est injective.
Il reste à prouver qu'elle est surjective, c'est-à-dire que pour tout réel a, il existe effectivement une forme n-linéaire alternée pour laquelle f(e1,...,en) = a.
Pour construire un tel f on pose bien entendu
- on a bien f(e1,...,en) = a.
- la n-linéarité se vérifie pour chacun des termes de la somme pris séparément. À chaque fois on a affaire à un produit de composantes, une pour chaque vecteur du n-uplet. Donc si un seul vecteur varie, on lit cela comme une composante du vecteur variable fois une constante ; c'est bien linéaire.
- le caractère alterné est moins évident. Si xi = xj pour deux indices i et j distincts, on introduit la transposition τ qui échange i et j. On regroupe les termes deux par deux : chaque permutation paire σ avec la permutation
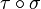
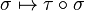
Mais les deux termes dont on fait la différence sont égaux, le résultat est donc bien nul.
On appelle notamment application déterminant relativement à la base base e1, ..., en l'unique application n-linéaire alternée telle que f(e1,...,en) = 1. Ses propriétés sont étudiées dans l'article déterminant (mathématiques).
Forme k-linéaire alternée en dimension n
Reprenant le cas d'une application k-linéaire alternée en dimension n, une partie seulement des résultats précédents peut être étendue. Il est toujours possible de supprimer les termes où figurent deux fois le même vecteur, il vient
où J est l'ensemble des k-uplets
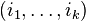
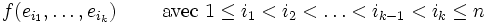
- si k = n alors il n'est pas possible de trouver de tels k-uplets, ce qui signifie qu'il n'existe pas d'autre forme k-linéaire alternée en dimension n que la forme nulle.
- si
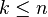
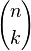
En définitive, l'espace des formes k-linéaires alternées sur un espace de dimension n est de dimension
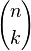
Plus précisément la formule de décomposition peut être écrite en utilisant la notion de déterminant : chaque coefficient est un mineur de la matrice représentative des vecteurs xi dans la base des ej.
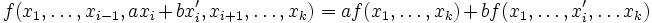
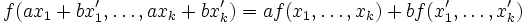
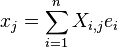
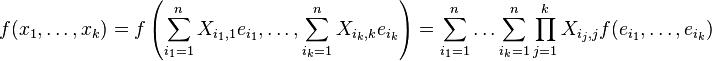
![[\exists i\neq j, x_i=x_j] \Rightarrow f(x_1,\dots, x_k)=0](https://static.techno-science.net/illustration/Definitions/autres/e/eab9accb712da0bdb0f0b9894eabb763_242f149306712dbadd46646bb24ec763.png)