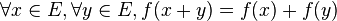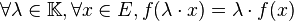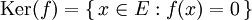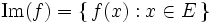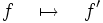Application linéaire - Définition
En mathématiques, une application linéaire (aussi appelée opérateur linéaire ou transformation linéaire) est une application entre deux espaces vectoriels qui respecte l’addition des vecteurs et la multiplication scalaire définie dans ces espaces vectoriels, ou, en d’autre termes, qui " préserve les combinaisons linéaires ".
Définitions
Soit
- ƒ : E → F
une application où E et F sont deux

- ƒ est une application linéaire (ou morphisme de

-
Une application possédant la première propriété est dite additive, et, pour la seconde, homogène.
- ƒ est un isomorphisme si :
- ƒ est un morphisme
- ƒ est bijective
- ƒ est un endomorphisme si :
- ƒ est un morphisme
- F = E
- ƒ est un automorphisme si :
- ƒ est un endomorphisme
- ƒ est bijective
- Si
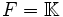
On note
- l’ensemble des applications linéaires de E dans F ;
-
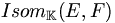
-
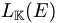
-
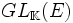
Comme son nom l'indique, le groupe linéaire, muni de la composition, est un groupe.
Noyau et Image
Si ƒ est une application linéaire de E dans F, on définit le noyau de ƒ, noté Ker(ƒ) (kern signifie " noyau " en allemand), et l’image de ƒ, notée Im(ƒ), par
ker(ƒ) est un sous-espace vectoriel de E et im(ƒ) est un sous-espace de F.
La formule suivante, valable pour un espace E de dimension finie, est souvent utile :
-
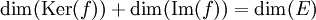
Elle est aussi appelée théorème du rang.
Le nombre dim( Im(ƒ) ) est aussi appelé rang de ƒ et est noté rg(ƒ). Si E et F sont de dimension finie et ƒ est représenté par la matrice A, alors le rang de ƒ est égal au rang de la matrice A ; une telle applicaiton linéaire est un tenseur d'ordre 2, une fois covariant, une fois contravariant.
Exemples
- la fonction linéaire " habituelle " :
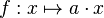
- les combinaisons linéaires de vecteurs
- l’application dérivation :
- d :
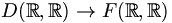
-
- d :