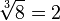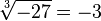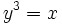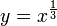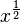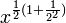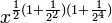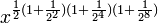Racine cubique - Définition
En mathématiques, la racine cubique d'un nombre réel y est l'unique nombre x qui, élevé à la puissance 3 (c'est-à-dire multiplié par lui-même trois fois) vaut y ; en d'autres termes, y = x3. La racine cubique de y est notée
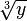
Par exemple, la racine cubique de 8 est 2, car 2 × 2 × 2 = 8. La racine cubique tient son nom du cube : la racine cubique du volume d'un cube est la longueur des arêtes. On écrit :
Un autre exemple, la racine cubique de -27 est -3, car (-3) × (-3) × (-3) = -27
Une racine cubique d'un nombre complexe z est un nombre u qui élevé au cube donne z; c'est-à-dire tel que u3 = z.
Tout nombre complexe non nul admet trois racines cubiques distinctes.
Formellement, la racine cubique d'un nombre réel (ou complexe) x est un réel (ou complexe) y solution de l'équation :
que l'on peut également noter lorsque y est réel strictement positif avec un exposant :
La racine cubique est associative avec les exposants, distributive avec la multiplication et la division, mais pas avec l'addition ou la soustraction.
Un complexe non nul possède trois racines cubiques. Un nombre réel possède une unique racine cubique réelle, mais on peut en trouver deux autres complexes, conjuguées l'une de l'autre, si l'on se place dans le domaine complexe.
Par exemple, les racines de l'unité (1) sont :
- 1, j= et j²=
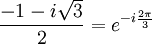
On a alors la relation: 1+j+j²=0
Si R est une racine d'un nombre réel ou complexe, les deux autres racines peuvent être retrouvées en multipliant R par les deux racines cubiques complexes de l'unité.
Calcul facile de la racine cubique
Une méthode simple permet de calculer la racine cubique d'un nombre en n'utilisant qu'une simple calculette non scientifique.
- Entrer le nombre dont la racine cubique est désirée
- Appuyer une fois sur le bouton racine carrée
- Appuyer une fois sur le bouton multiplication
- Appuyer deux fois sur le bouton racine carrée
- Appuyer une fois sur le bouton multiplication
- Appuyer quatre fois sur le bouton racine carrée
- Appuyer une fois sur le bouton multiplication
- Appuyer huit fois sur le bouton racine carrée
- Appuyer une fois sur le bouton multiplication
- ...
Répéter ainsi jusqu'à ce que l'affichage soit 1 (et donc ne change plus). Appuyer une fois encore sur multiplication puis une (seule) dernière fois sur le bouton racine carrée. Le chiffre qui s'affiche alors est une approximation — très proche — de la racine cubique du nombre initial.
Principe de la méthode
Il est possible de démontrer que
-
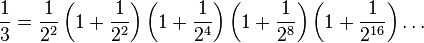
Après avoir élevé x à la puissance 1/3 en utilisant la relation précédente, nous obtenons:
-
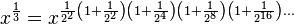
Le membre de gauche est la racine cubique de x.
Les différentes étapes de cette méthode sont:
À la première étape:
À la quatrième étape:
À la sixième étape:
À la huitième étape:
etc.
Après avoir calculé un nombre suffisant de termes selon la précision de la machine à calculer, l'extraction de la dernière racine carrée donne le membre de droite de la relation (*).