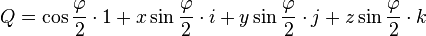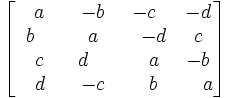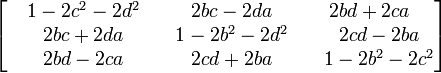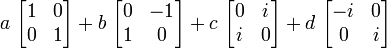Quaternion - Définition
Les quaternions, notés
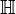
Origines et principes
Histoire
Les quaternions furent découverts par William Rowan Hamilton en 1843 à partir des travaux de Carl Friedrich Gauss et au siècle précédent Leonhard Euler. Il étudiait alors l'interprétation géométrique de l'arithmétique de nombres complexes dans le plan et cherchait à obtenir des résultats analogues dans l'espace à trois dimensions.
Après des années de recherches sur la construction d'une algèbre avec des " triplets " de trois nombres réels, il butait sur la multiplication, et en particulier la conservation des normes (Georg Ferdinand Frobenius a démontré en 1877 qu'une telle multiplication de triplets était impossible à définir).
Il eut alors l'idée d'utiliser des " quadruplets " en employant une dimension supplémentaire. Selon ses dires, il marchait un jour dehors le long du canal royal, avec son épouse quand soudain lui vint à l'esprit la solution sous la forme des relations :
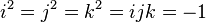
La théorie a été généralisée, d'autres ensembles comme les octonions découverts par la suite. Un élément d'un ensemble de cette nature fut qualifiée de nombre hypercomplexe jusqu'à la Première Guerre mondiale. Ces ensembles sont maintenant considérés comme des exemples d'algèbres semi-simples. Le théorème d'Artin-Wedderburn fournit une méthode de construction générique, elle se fonde sur la théorie des représentations d'un groupe fini. La construction des quaternions est donnée dans l'article représentations du groupe des quaternions. Elle correspond à l'unique algèbre simple fidèle de la représentation du groupe de quaternion sur le corps des nombres réels.
Principe
Hamilton décrivit un quaternion comme quadruplet de nombres réels, le premier élément étant un " scalaire ", et les trois éléments restants formant un " vecteur ", ou " imaginaire pur ".
Il put ainsi définir une multiplication avec les bonnes propriétés. Celle-ci peut se résumer à cette table de multiplication :
| · | 1 | i | j | k |
| 1 | 1 | i | j | k |
| i | i | -1 | k | -j |
| j | j | -k | -1 | i |
| k | k | j | -i | -1 |
Tout quaternion H peut être considéré comme une combinaison linéaire des quatre quaternions "unités" 1, i, j, et k :
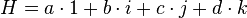
(où a, b, c, d sont des nombres réels).
H peut également s'écrire: H = z + z'·j (avec z et z' des nombres complexes de la forme a + b·i)
Les nombres réels a, b, c et d sont caractéristiques de H : il n'existe qu'une seule façon d'écrire H sous cette forme, et tout quaternion comportant ces mêmes 4 caractéristiques est nécessairement égal à H (la réciproque est vraie).
a s'appelle la composante réelle ou scalaire de H, tandis que b, c et d sont les composantes complexes de H. On dit aussi que a est le scalaire de H et que le triplet {b, c, d} ou [
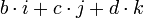
Cette découverte entraîna l'abandon de l'utilisation exclusive des lois commutatives, une avancée radicale pour l'époque. Les vecteurs et les matrices faisaient encore partie du futur, mais Hamilton venait en quelque sorte d'introduire le produit vectoriel et le produit scalaire des vecteurs.
Propriétés mathématiques
Relatives aux autres classes de nombres
L'algèbre des quaternions n'est plus commutative, mais partiellement anticommutative : 1 · i = i · 1 = i mais i · j = k et j · i = -k.
|
Cette non commutativité est d'ailleurs tout à fait compatible avec une interprétation géométrique des quaternions, par exemple les rotations vectorielles du plan sont commutatives, mais celles de l'espace ne le sont pas :
|
Somme
La somme de 2 quaternions
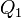
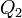
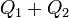
- si
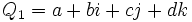
- si
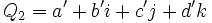
La somme est commutative et associative.
Opposé
Les quaternions
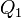
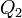
Dans ce cas, on écrit :
Produit
Le produit de 2 quaternions Q1 et Q2, noté
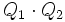
-
- si
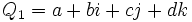
- si
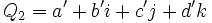
- si
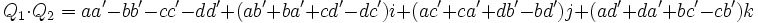
-
- qui peut encore s'écrire :
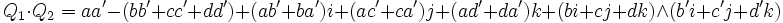
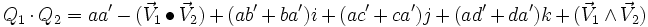
la dernière formule utilisant à la fois le produit scalaire (symbole

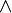
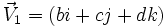
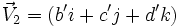
Le produit est associatif mais, comme on l'a dit plus haut, il n'est pas (sauf exceptions) commutatif !
Le produit est distributif par rapport à l'addition :
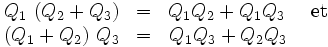
Scalaire
Un scalaire
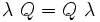
Conjugaison
On définit le conjugué (noté * ) du quaternion :
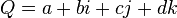
Le produit de
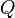
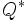
qui est le carré de la norme
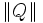
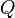
Norme et quaternions unitaires
Lorsque la norme
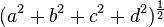
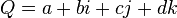
Nous verrons ci-dessous qu'on peut établir une sorte de correspondance entre un quaternion unitaire et une rotation vectorielle dans l'espace euclidien de dimension 3, et que cette particularité permet une représentation très simple du produit de deux rotations vectorielles.
Inverse
Si le quaternion
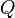
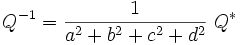
Division
Le produit étant non commutatif, on peut définir deux façons de diviser le quaternion
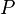
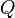
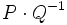
seconde façon :
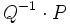
Conjugué d'un inverse, conjugué de la somme et du produit de deux quaternions
On montre aisément les égalités :
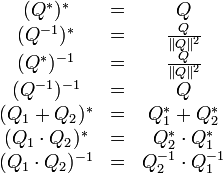
La notation (a, V)
Le quaternion
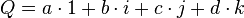

On écrit :
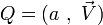
Cette notation permet de définir la somme et le produit de la façon suivante :
|
|
Elle permet aussi de re-définir ou définir les 3 notions suivantes :
- le conjugué
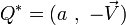
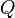
- le produit scalaire de deux quaternions :
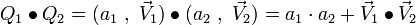
d'où l'on déduit :
- la norme d'un quaternion :
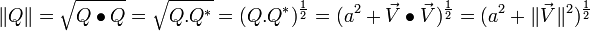
nota : le produit scalaire défini ci-dessus est commutatif et il est donc bien sûr différent du produit de quaternions défini plus haut.
Soit à présent un quaternion
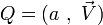
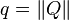
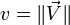
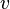
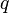
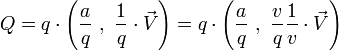
Or
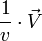
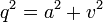
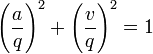
Il en résulte qu'il existe :
- un angle
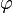


- un vecteur normé
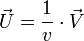
qui sont tels que l'on puisse écrire le quaternion
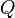
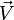
|
|
Cette façon d'écrire un quaternion est importante : les termes du couple,
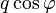
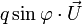
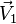
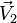
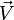
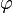

Les similitudes de l'espace et les quaternions
Pour démystifier les quaternions, nous allons faire un petit détour instructif par la géométrie élémentaire et en particulier par les similitudes dans l'espace. Une similitude dans
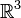
- d'un axe de rotation bien orienté (un vecteur unitaire U),
- d'un angle 2φ défini à 2kπ près et
- d'un rapport d'homothétie k, un réel strictement positif.
L'effet d'une similitude sur tous les vecteurs peut être considéré grossièrement comme un vissage avec expansion.
Voyage et trajets
Plus précisément, l'image du transformé d'un vecteur V (dont l'origine est supposée située sur l'axe U) est obtenue d'abord par une multiplication (homothétie) de ce vecteur par k, suivi par une rotation d'angle 2φ autour de l'axe de rotation (on pourrait aussi commencer par la rotation et la faire suivre de l'homothétie, mais il faudrait modifier un peu les explications qui vont suivre...). Cette rotation fait tourner d'un angle 2φ l'extrémité du vecteur kV sur un cercle (C) centré sur l'axe et situé dans un plan perpendiculaire à U. Or sur ce cercle, il y a deux façons d'effectuer le trajet : soit en utilisant un arc, soit en utilisant son complémentaire, ces arcs ne pouvant pas malheureusement être distingués par la seule mesure 2φ + 2kπ.
C'est précisément cette difficulté que permet de résoudre la notion de quaternion. Schématiquement, on peut dire qu'un quaternion, c'est comme une similitude qui saurait distinguer les 2 trajets que peut emprunter la rotation associée.
Dans la vie courante, si pour un voyage entre deux localités L1 et L2, vous avez a priori deux trajets possibles, la distinction entre ces trajets peut être faite en désignant deux sites-étapes intermédiaires s1 et s2. Et en parlant du trajet s1 et du trajet s2, vous sous-entendrez les localités de départ et d'arrivée L1 et L2.
En conservant cette analogie, il nous faut donc définir deux points intermédiaires sur les deux arcs du trajet.
À mi-chemin
Les points situés à mi-chemin sont parfaits pour cette mission. En effet, si je divise l'angle de vecteurs 2φ + 2kπ par 2, j'obtiens deux angles distincts φ + 2kπ et φ-π + 2kπ. Or, si j'utilise la rotation d'axe U et d'angle φ + 2kπ, je définis un site-étape différent de celui que j'obtiens avec la rotation φ-π + 2kπ. Ainsi à la similitude sim(U, 2φ, k), il correspond deux trajets distincts qui sont représentés par les deux quaternions distincts quat(U, φ, k) et quat(U, −π+φ, k).
Le formalisme
Le triplet (U, φ, k) peut s'écrire de façon équivalente sous la forme du couple (kcos(φ), ksin(φ)?U) de la notation (a, V). Et en utilisant des vecteurs a et b orthogonaux à U convenables, il est facile de montrer que ce couple prend la forme (a.b, a^b). Ainsi, nos sites-étapes nous permettent de revenir à des opérations très simples sur des vecteurs. Et comme ces opérations sont riches de propriétés remarquables, on sait définir (comme on l'a vu ci-dessus) une multiplication et une addition des quaternions. Vous pouvez " voir " ces deux opérations sur les quaternions ici : http://www.alcys.com
A signaler qu'une voie de recherche prometteuse peut être consultée sur le site (lien). On y définit justement la similitude dans l'espace à trois dimensions par un bivecteur qui est au couple de vecteurs ce que le vecteur est au couple de points. La loi de composition introduite dans ces bivecteurs est effectivement non commutative, et la restriction de cet ensemble au plan est l'ensemble des complexes.
Double produit de quaternions
De même que l'on peut calculer un double produit vectoriel, il est possible de calculer un double produit de quaternions.
Correspondance entre quaternion unitaire et rotation vectorielle
On peut démontrer que le transformé
![\vec V' = \mathbf R_{\left[2\varphi, \vec N\right]}(\vec V) \,](https://static.techno-science.net/illustration/Definitions/autres/5/5d416c2b9af7eb7a1b168bfcc1b35300_c7ea6e63c364e21d14b630f7315e4230.png)
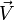
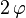
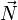
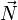
|
|
où
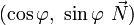
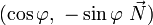
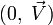
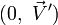
On peut aussi écrire cette transformé avec la notation
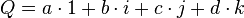
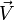

|
|
Composition de rotations vectorielles et produit de quaternions
La propriété précédente justifie le fait que l'on a coutume de dire, mais de façon peu rigoureuse, que le quaternion
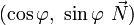
En utilisant le même langage approximatif, on peut dire que la composition de deux rotations successives
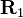
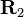
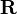
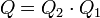
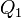
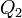
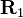
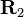
Montrons-le !
En posant :
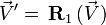
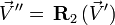
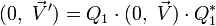
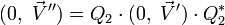
![(0,\ \vec V'') = Q_2\cdot \left[Q_1\cdot (0,\ \vec V)\cdot Q^*_1\right]\cdot Q^*_2](https://static.techno-science.net/illustration/Definitions/autres/b/b999ec46005e5d488ffeebdd64c524a5_b17ca9829e24cae324a24067c5257267.png)
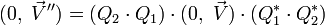
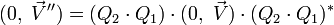
Ce qui établit la propriété annoncée pour la composition de deux rotations et que nous écrirons :
![\Bigg(0,\ \mathbf R_{\left[2\varphi_2, \vec N_2\right]}\left(\mathrm R_{\left[2\varphi_1, \vec N_1\right]} (\vec V)\right)\Bigg) = (\cos \varphi_2,\ \sin \varphi_2\ \vec N_2) \cdot (\cos \varphi_1,\ \sin \varphi_1\ \vec N_1) \cdot (0,\ \vec V) \cdot (\cos \varphi_1,\ -\sin \varphi_1\ \vec N_1) \cdot (\cos \varphi_2,\ -\sin \varphi_2\ \vec N_2)](https://static.techno-science.net/illustration/Definitions/autres/1/1087ff1423ed4d32a168f8287e4ea877_87d68c05d231ecaceef366fdfebae52d.png)
Notations matricielles
De même qu'il est possible de mettre en correspondance le nombre complexe
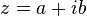
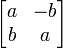
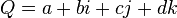
|
|
ou encore avec la matrice réelle suivante :
|
|
Il existe plusieurs représentations matricielles d'un quaternion. La matrice précédente en est une[1]. Celle qui suit est plus souvent utilisée. Ainsi, la matrice réelle créée à partir d'un quaternion s'écrit de cette façon (en gardant q=a+ib+jc+kd):
Si le quaternion unitaire représente une rotation depuis l'origine, on peut le représenter à l'aide d'une matrice 3x3
|
|
Avec ces équivalences, la somme et le produit de deux quaternions correspondent respectivement à la somme et au produit des matrices qui leur correspondent.
Remarque :
La matrice complexe
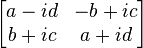
|
|
où les 4 matrices :
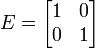
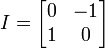
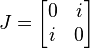
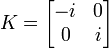
Applications
Alors que cela est discutable en dimensions trois, les quaternions ne peuvent pas être employés dans d'autres dimensions ( bien que des extensions comme celles des biquaternions et des algèbres de Clifford soient utilisables ). De toute façon, la notion de vecteur avait presque universellement remplacé celle des quaternions en science et en technologie dans le milieu du XXe siècle.
Aujourd'hui, les quaternions trouvent leur place en infographie, en théorie de la commande, dans le traitement du signal, dans la commande de mouvement et la mécanique orbitale, principalement pour représenter les rotations et les orientations en dimension trois. Par exemple, il est fréquent que les systèmes de commande de déplacement d'un vaisseau spatial soient régis en termes de quaternions. La raison est qu'effectuer beaucoup d'opérations sur les quaternions est numériquement plus stable que d'effectuer beaucoup d'opérations sur les matrices.
Interpolation de rotations
Si l'on prend 2 rotations de l'espace ra et rb, l'interpolation linéaire de ces roations n'est en général pas une rotation. Pour pouvoir interpoler, il faut soit
- utiliser les angles d'Euler,
- utiliser les quaternions.
Dans le dernier cas, les 2 rotations sont représentées par 2 quaternions qa et qb sur la sphère unité S4, et l'interpolation correspond à la géodésique entre ces 2 points
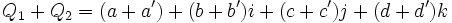
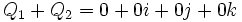
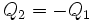
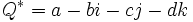
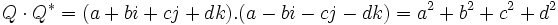
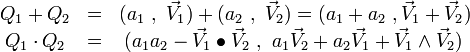
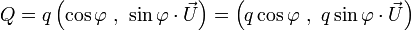
![(0,\ \vec V') = \left(0,\ \mathbf R_{\left[2\varphi, \vec N\right]}(\vec V)\right) = (\cos \varphi,\ \sin \varphi\ \vec N)\cdot (0,\ \vec V)\cdot (\cos \varphi,\ -\sin \varphi\ \vec N)](https://static.techno-science.net/illustration/Definitions/autres/c/c45d7dbec8f7e7b7940a0654a7b2cfae_d7300a40d6251c1a5512283113b609a2.png)