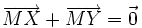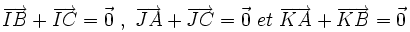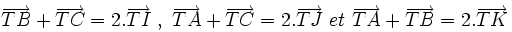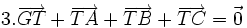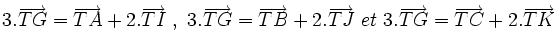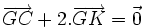Triangle - Définition
En géométrie euclidienne, un triangle est une figure plane, formée par trois points en général supposés non alignés, et par les trois segments qui les relient. La dénomination de " triangle " est justifiée par la présence de trois angles dans cette figure, ceux formés par les segments entre eux. Les trois points sont les sommets du triangle, les trois segments ses côtés, et les trois angles ses angles.
Un triangle peut aussi être défini comme un polygone à trois côtés, ou encore comme un polygone à trois sommets. Après le point et le segment, le triangle est la figure polygonale la plus simple.
On qualifie de triangles dégénérés les triangles avec un angle plat (de 180°) (on parle alors de triangle plat), les triangles avec deux angles nuls (de 0°), et les triangles avec un angle nul (de 0°) et deux angles droits (de 90°), sont qualifiés de triangles en aiguille. Dans la suite de cet article, on suppose que les triangles ne sont pas dégénérés, car ils ne vérifient pas la plupart des propriétés attribuées aux triangles.
La plupart des propriétés et définitions énoncées dans cet article étaient déjà énoncées d'Euclide, environ 300 ans avant Jésus-Christ, comme en atteste son ouvrage, "Éléments de géométrie".
Pour l'étude du triangle dans d'autres géométries, voir Triangle (géométries non euclidiennes).
Convention d'écriture
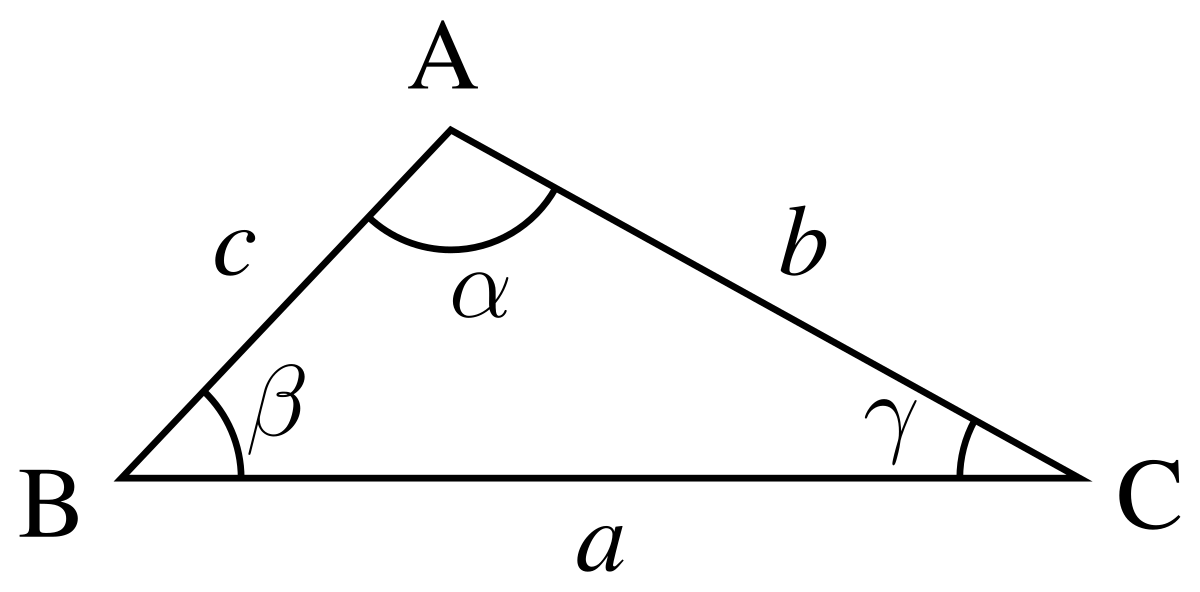
Comme tout polygone, on nomme un triangle en citant le nom de ses sommets, par exemple ABC. En général, pour nommer les longueurs des côtés, on utilise le nom de l'angle opposé, en minuscules : a = BC, b = AC, c = AB. On nomme les angles en utilisant des lettres grecques minuscules ou le nom du sommet surmonté d'un accent circonflexe :
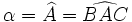
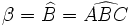
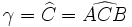
Nous utiliserons ces notations dans cet article.
Propriétés élémentaires
Triangle et autres polygones
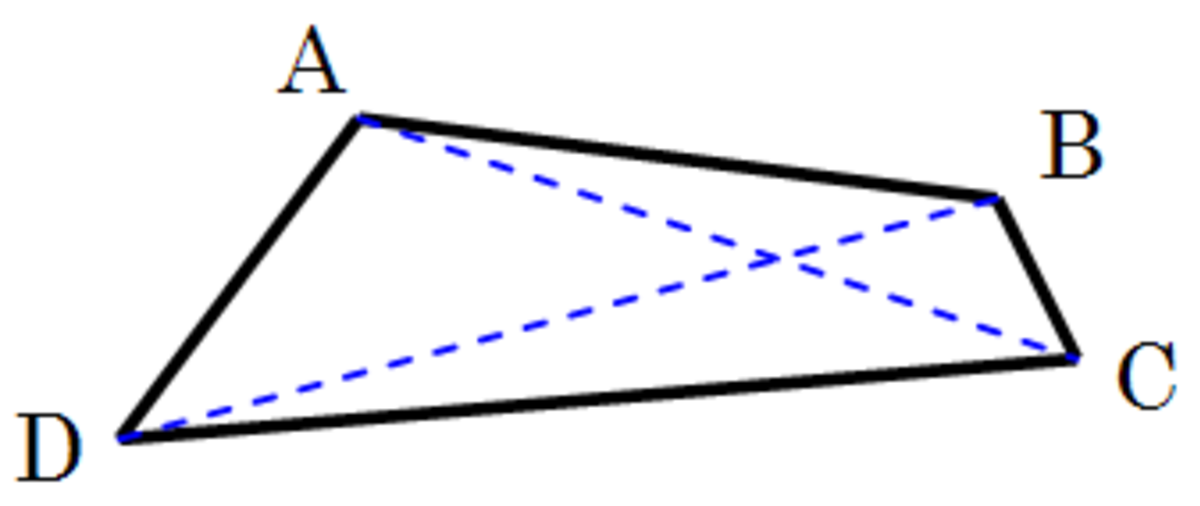
Le triangle est le plus simple des polygones. C'est le seul qui ne possède pas de diagonale. Dans l'espace, il n'est pas nécessaire de s'assurer que trois points sont coplanaires pour obtenir un triangle, alors que, par exemple, si quatre points coplanaires forment un quadrilatère, quatre points non coplanaires ne forment pas un polygone, mais un tétraèdre :
D'autre part, tout polygone peut être " découpé " en triangles (on dit que ces triangles forment une partition de ce polygone), le nombre minimal de triangles étant n − 2, où n est le nombre de côtés du polygone. On voit que l'étude des triangles est fondamentale pour celle des autres polygones, par exemple pour la démonstration du théorème de Pick.
Longueurs des côtés
La somme de deux longueurs de côtés d'un triangle est toujours strictement supérieure au troisième côté. Autrement dit, on a toujours, dans un triangle ABC :
- a + b > c ;
- a + c > b ;
- b + c > a.
Réciproquement, étant donnés trois nombres réels a, b et c tels que a < b < c, si a + b > c, alors il existe un triangle dont les côtés mesurent a, b et c.
La somme des longueurs des trois côtés d'un triangle est appelée son périmètre.
Somme des angles
La somme des mesures des angles d'un triangle est égale à la mesure de l'angle plat, soit 180° ou π radians.
Ceci se démontre en traçant la parallèle à AB passant par C et en utilisant les propriétés des angles entre deux droites parallèles (c'est la démonstration d'Euclide dans ses Éléments, proposition I-32).
Sur la figure ci-dessus, les angles codés en bleu sont égaux, car alternes-internes. Les angles codés en vert sont de même égaux. D'autre part, la somme des trois angles de sommet C est l'angle plat. Donc la somme d'un angle rouge, d'un vert et d'un bleu (en particulier ceux du triangle) est l'angle plat.
Typologie des triangles
Classement suivant le type d'angles
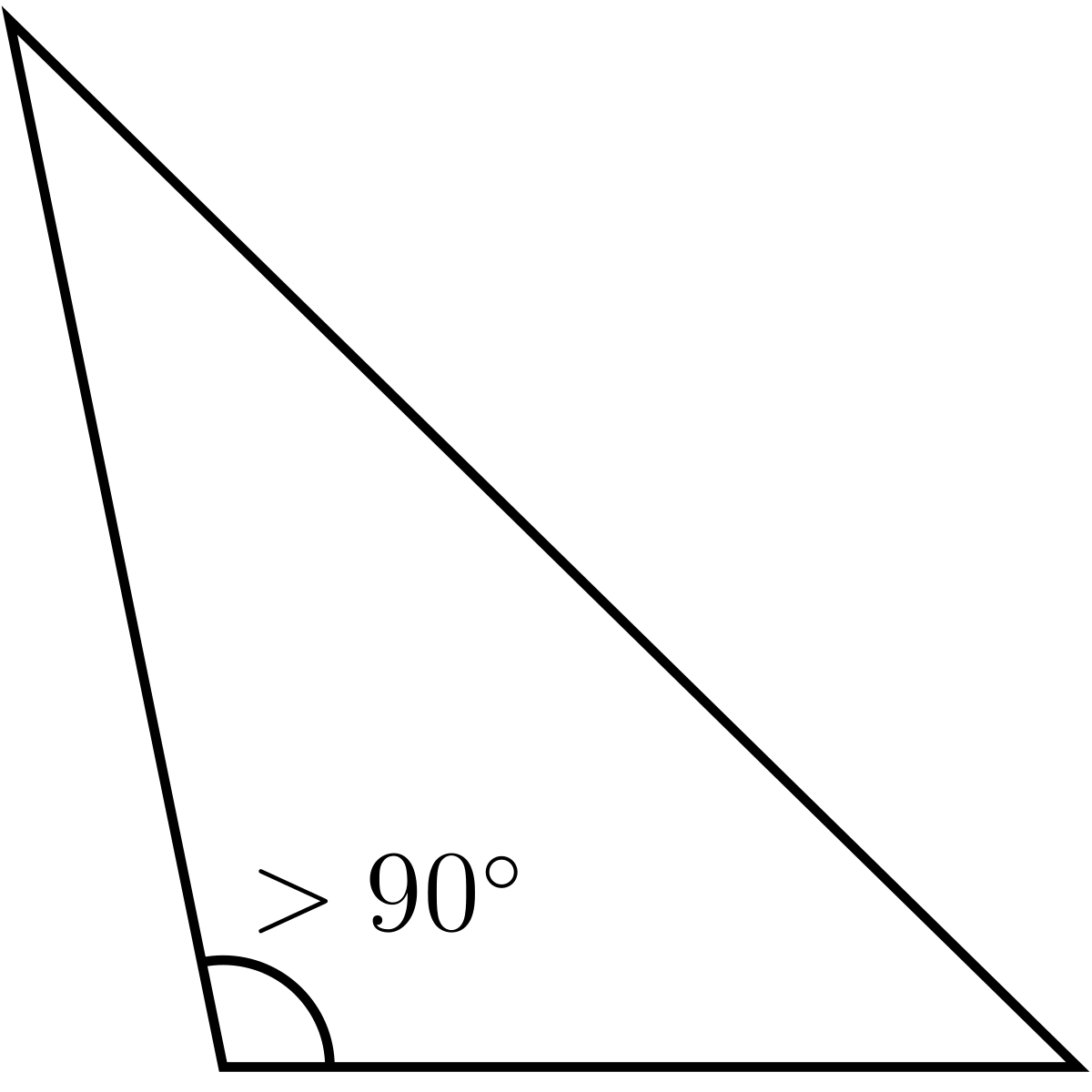
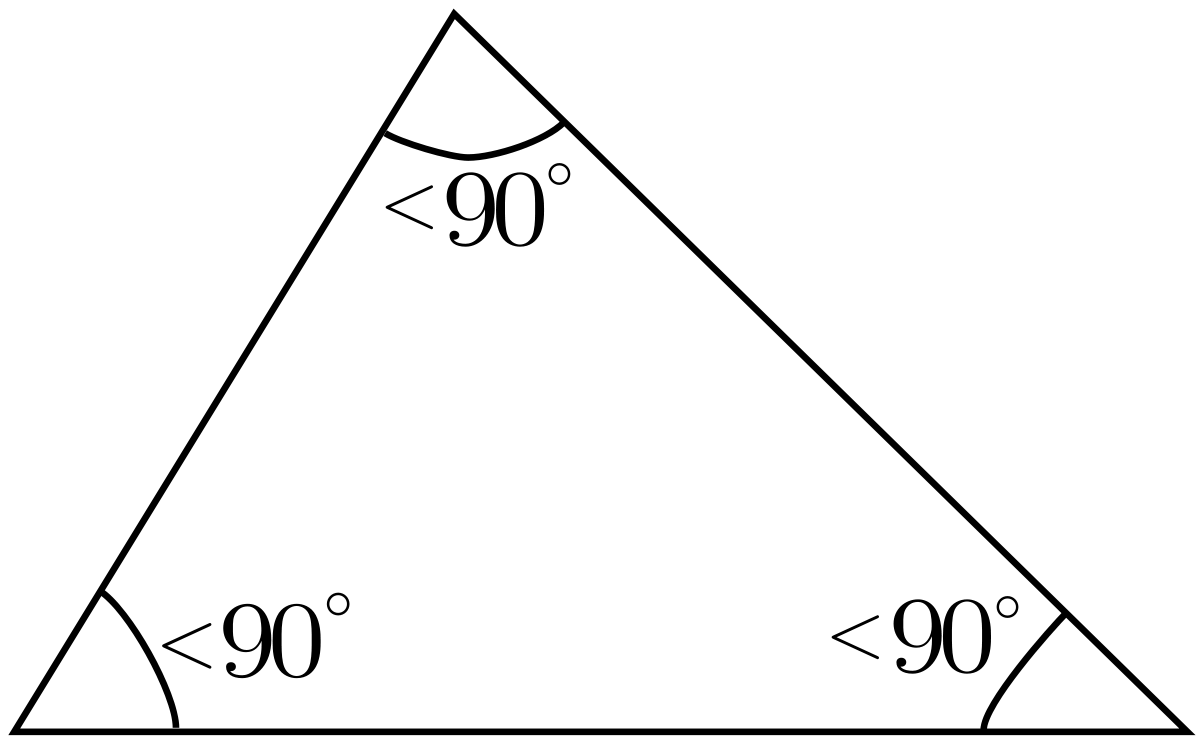
Comme la somme des angles d'un triangle vaut 180°, un triangle ne peut pas comporter deux angles droits (mesurant 90°) ou obtus (mesurant plus de 90°). Il a donc au moins deux angles aigus. Si le troisième angle est :
- droit, on parle de triangle " rectangle " ;
- obtus, on parle de triangle " obtusangle " (ou parfois de triangle obtus) ;
- aigu, on parle de triangle " acutangle " (ou de triangle aigu).
Triangle rectangle
Les deux propositions suivantes sont équivalentes :
- Un triangle admet un angle droit.
- Le carré du plus grand côté d'un triangle est égal à la somme des carrés des deux autres côtés.
(Cette équivalence est appelée Théorème de Pythagore).
Dans ce cas, le triangle est dit rectangle.
Le côté le plus grand d'un triangle rectangle est appelé hypoténuse.
Triangle 3-4-5
C'est un triangle rectangle dont les côtés forment une progression
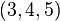
Ce cas particulier d'un triangle rectangle est connu depuis l'Antiquité. Il est facile à réaliser à l'aide d'une corde à treize nœuds : on l'utilise donc pour tracer un angle droit au sol. Pour cette raison, on l'appelle aussi " triangle des arpenteurs ".
Triangle 30-60-90
C'est un triangle rectangle dont les angles font 30°, 60° et 90°, c'est-à-dire forment une progression
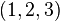
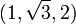
Ce triangle est parfois aussi appelé " triangle de l'écolier " : les équerres d'écolier ont parfois cette forme. On parle aussi de " triangle hémi-équilatéral ". Cette dernière appellation se justifie en remarquant qu'un triangle équilatéral peut être coupé suivant un axe reliant l'un de ses sommets au milieu du côté opposé, pour donner deux triangles 30-60-90 égaux.
Demi-carré
Un triangle peut être à la fois rectangle et isocèle. Dans ce cas, il l'est obligatoirement par le même sommet. Ses deux angles aigus mesurent 45° (ou π/4 rad).
C'est le triangle obtenu en divisant un carré en deux suivant sa diagonale, d'où le nom du triangle : " demi-carré ".
Classement suivant les symétries
Les triangles peuvent se classer suivant plusieurs types de symétries :
- suivant le nombre de côtés égaux ;
- suivant le nombre d'angles égaux ;
- suivant le nombre d'axes de symétrie présents ;
- suivant le type de symétrie présent ;
- suivant le type des angles (aigus, droits ou obtus).
En fait, tous ces classements, sauf le dernier, sont équivalents.
Triangle isocèle
Les propositions suivantes sont équivalentes :
- Un triangle a deux côtés de même longueur.
- Un triangle a deux angles de même mesure.
- Un triangle a un axe de symétrie.
Dans ce cas le triangle est dit isocèle. (On peut aussi dire isoangle).
Lorsqu'un triangle ABC est tel que AC = AB (les deux côtés d'extrémité A sont égaux), alors on dit que le triangle est isocèle de sommet A. A est le sommet principal du triangle. Le côté [BC], opposé à A, est appelé base du triangle.
Lorsqu'un triangle est isocèle en A, la hauteur issue de A est à la fois hauteur, médiatrice, médiane et bissectrice.
Triangle équilatéral
Les propositions suivantes sont équivalentes :
- Un triangle a ses trois côtés de même longueur.
- Un triangle a ses trois angles de même mesure.
- Un triangle a trois axes de symétrie (bien que deux axes de symétrie suffisent).
Dans ce cas le triangle est dit équilatéral, ou équiangle. Un triangle équilatéral peut-être vu comme un triangle isocèle particulier.
Triangle scalène
Un triangle scalène (du grec skalenos : boîteux, inégal, déséquilibré, oblique...) est un triangle :
- dont les trois côtés sont de longueurs différentes ;
- ou dont les trois angles sont de mesures différentes ;
- ou encore qui n'a pas d'axe de symétrie.
Les trois définitions ci-dessus sont équivalentes entre elles. Un tel triangle n'est bien sûr ni isocèle, ni équilatéral.
Triangle bisocèle
Un triangle bisocèle est un triangle isocèle qui, lorsqu'il est "coupé" en deux par la bissectrice d'un de ses angles, forme deux triangles isocèles eux aussi. Il n'y a que deux cas de triangles bisocèles : le triangle d'or et le triangle isocèle rectangle.
Lien externe : démonstration.
Éléments remarquables du triangle
Médianes et centre de gravité
On appelle " médiane " d'un triangle chacune des trois droites passant par un sommet du triangle et par le milieu du côté opposé à ce sommet.
- Propriété
- Chacune des trois médianes divise le triangle en deux triangles d'aires égales.
Considérons les deux triangles ABI et ACI (voir figure).
On appelle H le projeté orthogonal du point A sur la droite (BC).
Comme I est le milieu du segment [BC], on a BI = CI.
L'aire du triangle ABI est égale à
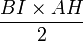
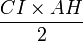
On démontre de la même manière que les médianes issues de B et de C vérifient cette propriété.
- Propriété
- Les trois médianes d'un triangle sont concourantes. Leur point d'intersection

- Par définition, le milieu M d'un segment [XY] est le point de ce segment à égale distance de ses extrêmités. Il vérifie donc la relation vectorielle :
(ce qui signifie que M est aussi l'isobarycentre des extrémités du segment [XY]).
- Appelons I, J et K les milieux respectifs des trois côtés [BC], [AC] et [AB]. D'après ce qui précède :
- Soit T le point intersection des deux médianes (AI) et (BJ). Nous déduisons de la ligne ci-dessus :
- Considérons à présent l'isobarycentre G des 3 points A, B et C. Par définition, il vérifie la relation vectorielle :
Nous en déduisons :
puis, en utilisant les égalités précédentes concernant T :
Comme T appartient à (AI), T, A et I sont alignés ; donc d'après la première égalité de la ligne précédente, G est aligné avec eux ; en d'autres termes, G appartient à (AI). On montre de la même manière que G appartient à (BJ). Autrement dit, G appartient à l'intersection de (AI) et de (BJ), qui se réduit à T. Bref, G et T sont confondus, et nous pouvons écrire, d'après la troisième égalité de la ligne précédente :
G, C et K sont donc alignés, ou, en d'autres termes, G appartient à (CK), la troisième médiane. Les trois médianes sont donc concourantes, CQFD.
- Propriété
- Il découle de la démonstration précédente que l'intersection des trois médianes est aussi l'isobarycentre des points A, B et C. De ce fait, si I désigne le milieu du côté [BC] on a la relation vectorielle :
-
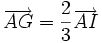
-
- Cette relation s'applique également aux deux autres sommets du triangle vis-à-vis du milieu de leur côté opposé.
Médiatrices et cercle circonscrit
On appelle " médiatrice " d'un triangle chacune des médiatrices de ses côtés [AB], [AC] et [BC].
- Propriété
- Les trois médiatrices d'un triangle sont concourantes en un point
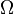
Notons Ω l'intersection des deux médiatrices des segments [AB] et [AC].
- Ω est sur la médiatrice de [AB] donc AΩ = BΩ.
- Ω est sur la médiatrice de [AC] donc AΩ = CΩ.
Donc CΩ = BΩ : par suite Ω est sur la médiatrice du segment [BC]. Les trois médiatrices sont donc concourantes en Ω.
- Propriété
- Il existe un et un seul cercle passant à la fois par les trois sommets du triangle. Ce cercle de centre
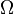
- Existence
- Elle a été prouvée ci-dessus : AΩ = CΩ = BΩ donc le cercle de centre Ω et passant par A passe aussi par B et C.
- Unicité
- Si un cercle passe à la fois par A et B, son centre appartient à la médiatrice de [AB]. S'il passe par A et C, son centre appartient à la médiatrice de [AC]. Donc, si un cercle passe par les trois points A, B et C, son centre appartient à la fois aux médiatrices de [AB] et de [AC], c'est-à-dire à leur intersection. Celle-ci se réduit à un point, Ω ; le cercle a donc nécessairement pour centre Ω. Le rayon du cercle est donc égal à AΩ. On a unicité du centre et du rayon, donc du cercle.
Bissectrices et cercle inscrit
Les bissectrices d'un triangle sont les trois bissectrices de ses angles.
- Propriété
- Les trois bissectrices d'un triangle sont concourantes en un point
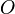
La bissectrice d'un angle est l'axe de symétrie de cet angle. Chaque point de la bissectrice est donc à égale distance des deux côtés de l'angle.
De ce fait, le point d'intersection O de deux bissectrices est à égale distance des côtés des deux angles correspondants, donc des trois droites (AB), (AC) et (BC).
Ce point est donc à égale distance des deux côtés du troisième angle, donc sur la troisième bissectrice : les trois bissectrices sont concourantes.
- Propriété
- Il existe un et un seul cercle intérieur au triangle et tangent à la fois à ses trois côtés. Ce cercle de centre
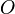
D'après la propriété précédente des bissectrices, on peut tracer, à l'intérieur du triangle, un cercle de centre O qui est tangent aux trois droites (AB), (AC) et (BC) : c'est le cercle inscrit dans le triangle. Il existe trois autres cercles ayant la même propriété (mais situés à l'extérieur du triangle) qu'on appelle cercles exinscrits du triangle.
- Voir Cercles inscrit et exinscrits d'un triangle

Remarque : les noms de hauteurs, médianes, médiatrices ou bissectrices désignent non seulement les droites indiqués ci-dessus, mais aussi les segments de ces droites intérieurs au triangle.
Hauteurs et orthocentre
On appelle " hauteur " d'un triangle chacune des trois droites passant par un sommet du triangle et perpendiculaire au côté opposé à ce sommet. L'intersection de la hauteur et du côté opposé s'appelle " pied " de la hauteur.
- Propriété
Les trois hauteurs d'un triangle sont concourantes. Leur point d'intersection

On considère l'homothétie de centre G centre de gravité du triangle, et de rapport -2. Elle transforme le triangle ABC en un triangle A'B'C'.
Le point I milieu de [BC] a pour image le point A qui est donc le milieu de [B'C']. La hauteur issue de A est perpendiculaire à [BC] donc est perpendiculaire à [B'C'] et passe par son milieu. C'est la médiatrice du segment [B'C'].
On démontre ainsi que les trois hauteurs du triangle ABC sont les trois médiatrices du triangle A'B'C'. Elles sont donc concourantes.

Relation d'Euler
Relation vectorielle d'Euler :
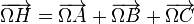
La définition vectorielle du centre de gravité permet d'écrire :
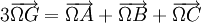
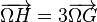
Autres éléments remarquables
Les trois points H, G et Ω sont alignés sur une droite appelée droite d'Euler du triangle et GH = 2ΩG (relation d'Euler).
Par ailleurs les milieux des trois côtés ainsi que les trois pieds des hauteurs sont sur un même cercle dénommé cercle d'Euler ou cercle des neufs points du triangle.
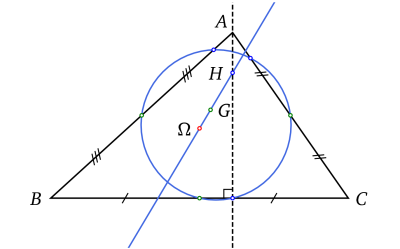
On peut dénombrer des centaines de points remarquables d'un triangle. Pour les plus fameux d'entre eux, voir l'article liste des éléments remarquables d'un triangle.
Propriétés en géométrie euclidienne
Aire d'un triangle
L'aire d'un triangle est l'aire de la portion du plan qu'il enferme. Il existe plusieurs manières de la calculer, selon les informations dont on veut partir.
À partir des longueurs des trois côtés

Comme un triangle rectangle peut-être obtenu en divisant en deux parties égales un rectangle selon sa diagonale, l'aire d'un triangle rectangle en A est simplement le demi produit des longueurs b et c soit
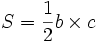
En traçant une hauteur d'un triangle quelquonque, on peut le décomposer en deux triangles rectangles. En utilisant la formule précédente, on trouve alors que l'aire d'un triangle est simplement la moitié du produit de la longueur de la hauteur h par la longueur du côté opposé (ici a) soit
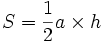
On peut aussi utiliser la formule de Héron d'Alexandrie :
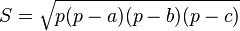
où
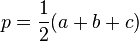
À partir des vecteurs
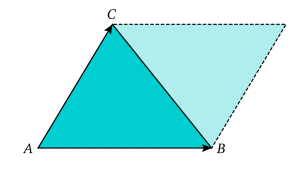
L'aire du parallélogramme défini par deux vecteurs
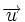
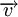
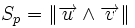
On peut calculer l'aire d'un triangle à partir de cette formule :
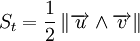
Relations métriques dans un triangle
Notations :
- p désigne le demi-périmètre du triangle :
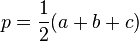
- S désigne la surface du triangle ;
- R désigne le rayon du cercle circonscrit ;
- h désigne la hauteur relative au coté BC de longueur a ;
- r désigne le rayon du cercle inscrit ;
-
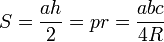
-
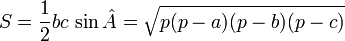
-
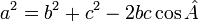
-
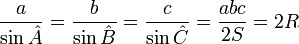
-
- Avec
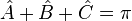
- Avec
Triangles semblables et isométriques
Deux triangles sont isométriques lorsque leurs trois cotés sont respectivement égaux ( égaux un à un )
Deux triangles sont semblables lorsque leurs trois angles sont respectivement égaux un a un.
Dans l'espace
Polyèdres à faces triangulaires
Le triangle est la forme des faces de nombreux polyèdres réguliers : tétraèdre (quatre faces qui sont des triangles équilatéraux, c'est la pyramide à base triangulaire), octaèdre (huit faces, les pyramides égyptiennes sont des demi-octaèdres), icosaèdre (vingt faces)...