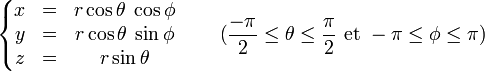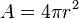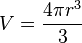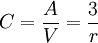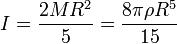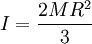Sphère - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs est disponible ici.

Une sphère dans un espace euclidien

Une sphère est une surface à 3 dimensions dont tous les points sont situés à une même distance d'un point appelé centre. La valeur de cette distance commune au centre est appelée le rayon de la sphère. Elle n'inclut donc pas les points situés à une distance inférieure au rayon, au contraire de la boule. Concrètement, on peut voir une sphère comme une coquille vide infiniment mince.

Une sphère approximative est appelée géosphère en référence à la Terre dont la surface n'est pas une sphère parfaite. Ce terme est fréquemment utilisé en astrophysique et parfois en architecture.

Dans un espace euclidien, il s'agit du ballon que tout le monde associe au terme de sphère. Dans un espace non-euclidien ou dans le cas de la définition d'une distance non euclidienne, la forme peut être plus complexe.

Une sphère peut aussi être définie comme la surface formée par la rotation d'un cercle autour de son diamètre. Si le cercle est remplacé par une ellipse, on obtient un sphéroïde.

En géométrie cartésienne, une sphère de centre (x₀, y₀, z₀) et de rayon r est l'ensemble des points (x, y, z) tels que

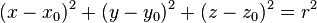
Les points de la sphère de rayon r et de centre l'origine du repère peuvent être paramétrés par

On peut voir $\theta\,$ comme la latitude et $\phi\,$ comme la longitude. (voir fonctions trigonométriques et coordonnées sphériques).

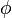
L'aire d'une sphère de rayon $r$ est:

Le volume qu'elle renferme est :

Sa compacité est de :

Le Moment d'inertie d'une sphère homogène pleine de rayon $R$ , de masse volumique $ρ$ , de masse M par rapport à un axe passant par son centre est:

Le Moment d'inertie d'une sphère homogène vide de rayon $R$ , de masse M par rapport à un axe passant par son centre est:

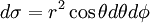
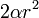
L'élément d'aire de la sphère de rayon $r\,$ dans les coordonnées latitude-longitude est $d\sigma=r^2\cos\theta d\theta d\phi\,$ . On en déduit que l'aire d'un fuseau (portion limitée par deux demi-cercles joignant les pôles et faisant un angle $\alpha\,$ exprimé en radians est $2\alpha r^2\,$ . Cela permet aussi de calculer l'aire d'une calotte sphérique (on dit aussi segment de sphère), c’est-à-dire d'une portion de sphère limitée par deux plans parallèles de distance $h\,$ l'un pouvant être tangent à la sphère. 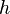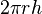On trouve $2\pi rh\,$ : l'aire est la même que celle d'un cylindre circulaire de même hauteur tangent à la sphère (cylindre circonscrit). Ce résultat remarquable était connu d'Archimède, qui aurait demandé qu'il soit mentionné sur son tombeau.

Le cylindre circonscrit à une sphère donnée a un volume égal à 3/2 fois le volume de la sphère.

La sphère a la plus petite aire parmi les surfaces renfermant un volume donné et renferme le volume le plus élevé parmi les surfaces d'une aire donnée. Pour cette raison, la sphère apparaît dans la nature, par exemple les bulles et gouttes d'eau (en l'absence de gravité) sont des sphères car la tension superficielle essaie de minimiser l'aire.