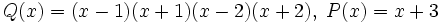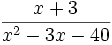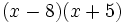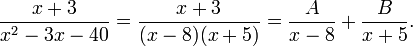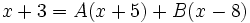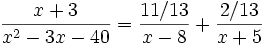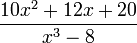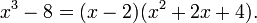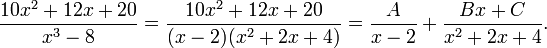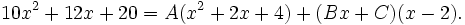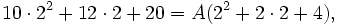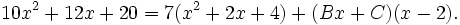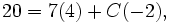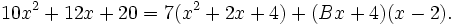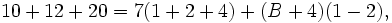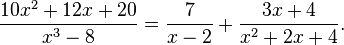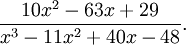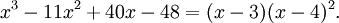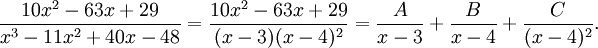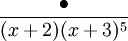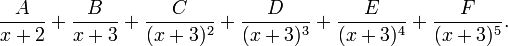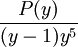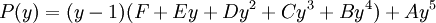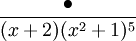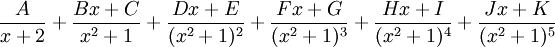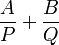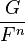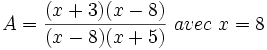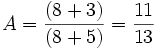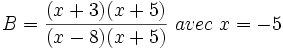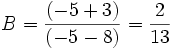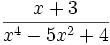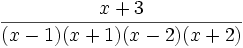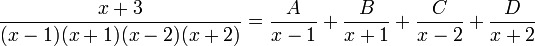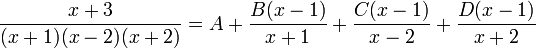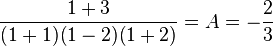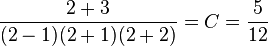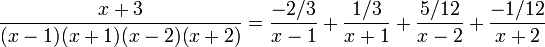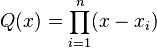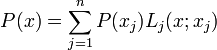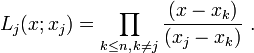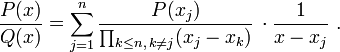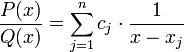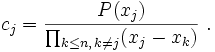Fraction partielle - Définition

En algèbre, la décomposition en fractions partielles ou en éléments simples d'une fonction rationnelle est son expression sous une somme de fractions ayant toutes un dénominateur irréductible et un numérateur de degré inférieur au dénominateur. Les fractions partielles sont utilisées dans le calcul intégral pour faciliter la recherche de primitives. Elles sont aussi utilisées pour calculer l'inverse des transformées de Laplace.

Déterminer quels polynômes sont irréductibles dépend du corps de scalaires utilisé. Ainsi, si on se limite aux nombres réels, les polynômes irréductibles auront un degré de 1 ou de 2. Si les nombres complexes sont utilisés, seuls les polynômes de premier degré seront irréductibles. De même, si on se limite aux nombres rationnels, on pourra trouver des polynômes de degré supérieurs à 2 irréductibles.

Exemples

Facteurs de premier degré distincts au dénominateur

Supposons qu'on recherche la décomposition en fractions partielles de la fonction rationnelle

Le dénominateur se factorise en

Nous cherchons donc les scalaires A et B tels que

Une façon de trouver A et B commence par l'élimination des fractions. Cela revient à multiplier chaque côté par le dénominateur commun : (x − 8)(x + 5). Ce qui nous donne

En prenant des valeurs judicieuses pour x, on obtient directement les valeurs de A et de B :

• pour x=8, le coefficient de B s'annule et il vient A = 11/13,
• pour x=-5, le coefficient de A s'annule et il vient B = 2/13.

Nous obtenons donc la décomposition en fractions partielles :

Facteur irréductible de second degré au dénominateur

Pour décomposer

en fractions partielles, observons d'abord

Le fait que x² + 2x + 4 ne soit pas factorisable en utilisant des coefficients réels est visible car le discriminant, 2² − 4(1)(4), est négatif. Nous cherchons donc des scalaires A, B, C tels que

Par l'élimination des fractions nous trouvons

Nous pouvons procéder comme dans l'exemple précédent. La substitution de 2 pour x élimine complètement le second terme et nous obtenons

par exemple, 84 = 12A, donc A = 7, ce qui nous donne

Ensuite, la substitution de 0 par x donne

alors C = 4. Nous avons maintenant

Substituons 1 par x, nous avons

donc B = 3. La décomposition en fractions partielles est

Répétition d'un facteur de premier degré au dénominateur

Considérons la fractions rationnelle

Par factorisation du dénominateur nous avons

La multiplicité du facteur de premier degré (x − 4) est supérieure à 1. Dans de tels cas, la décomposition en fractions partielles prend la forme

Répétition de facteurs au dénominateur: cas général

Pour une fonction rationnelle de la forme

(où "   " est un polynôme quelconque de degré inférieur à 5) la décomposition en fractions partielles aura comme allure

La détermination des coefficients A, B, C, D, E, F s'opère en effectuant le changement de variable y = x + 3. La fraction s'écrit alors

La division de P(y) par y - 1 suivant les puissances croissantes(voir polynôme) nous donne alors

Il suffit alors d'opérer la division et de revenir à la variable de départ.

Le patron général est facile à deviner, pour un fonction rationnelle de la forme

avec le facteur irréductible du second degré x² + 1 au dénominateur, la décomposition en fractions partielles sera de la forme

Le même genre de développement s'applique à tous les polynômes irréductibles du second degré.

Principe de base

Le principe de base est assez simple ; c'est plutôt le côté algorithmique qui réclamera de l'attention dans les cas particuliers.

Soit R(x) une fonction rationnelle de x qui admet une factorisation au dénominateur qu'on notera

P(x)Q(x)

sur un corps K (par exemple les nombres réels ou les nombres complexes). Si P et Q sont premiers entre eux, alors R peut s'écrire

pour certains polynômes A(x) et B(x) sur K. L'existence d'un telle décomposition est une conséquence du fait que l'anneau des polynômes sur K est un anneau euclidien dans lequel l'égalité

CP + DQ = 1

existe pour certains polynômes C(x) et D(x). On obtient ce dernier résultat par l'identité de Bézout.

L'utilisation de ce principe permet d'écrire R(x) comme une somme de fonctions rationnelles avec comme dénominateurs des puissances de polynômes irréductibles.

Enfin une fraction de la forme

peut s'écrire comme une somme de fractions dont le dénominateur est une puissance de F et dont les numérateurs sont de degrés inférieurs à F, plus, éventuellement un autre polynôme. Ceci peut être réalisé grâce à une succession de division euclidienne par F (la méthode est analogue à celle utilisée pour écrire un nombre en base a).

Quand K est le corps des nombres complexes, F est de degré 1 (théorème fondamental de l'algèbre) et les numérateurs sont donc constants. Quand K est le corps des nombres réels, le degré de F sera 1 ou 2 et les numérateurs seront linéaires ou constants.

Autres Exemples

• Soit le cas particulier que nous avions vu précédemment :

Ce qui donne :

Nous pouvons trouver les valeurs de A et B ainsi :

donc

On procède de la même façon pour B :

donc

• De même, prenons la fonction rationnelle

Par factorisation du polynôme bicarré et par utilisation des identités remarquables, on peut l'écrire

qui peut être transformée davantage:

Pour trouver le coefficient A, il suffit de multiplier les deux membres par x - 1 puis de remplacer x par 1

De même pour trouver B, il suffit de multiplier par x + 1 et de remplacer x par -1

Pour C, il suffit de multiplier par x - 2 et de remplacer x par 2

et pour D, on multiplie par x + 2 et on remplace x par -2

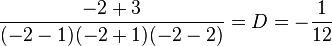
Donc

• Les exemples précédents peut être généralisés à la situation suivante:

Soit Q(x) un polynôme unitaire de degré n sur un corps K dont la décomposition en facteurs de premiers degrés est

où tout les x_i différents deux à deux. En d'autres mots, Q a des racines simples sur K. Si P(x) est un polynôme quelconque de degré , par la formule d'interpolation de Lagrange P(x) peut être écrit de manière unique comme un somme

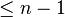
où est le polynôme de Lagrange

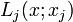
En divisant la représentation de Lagrange terme à terme par Q(x) dans sa forme factorisée on obtient

D'où on arrive à la décomposition en fractions partielles

de la fonction rationnelle avec les coefficients

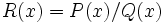
Le premier exemple peut être obtenu avec le cas particulier .