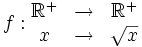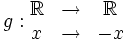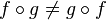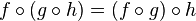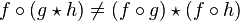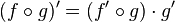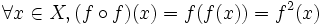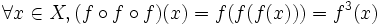Composition de fonctions - Définition

En mathématiques, une fonction composée, formée par la composition de deux fonctions, représente l'application de la première fonction au résultat de l'application de la seconde (à l'argument choisi).

Les deux fonctions f: X Y et g: Y Z peuvent être composées en appliquant f à l'argument x, puis en appliquant g au résultat. On obtient ainsi la fonction g o f: X Z définie par (g o f)(x) = g(f(x)) pour tout x de l'ensemble X.

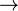
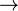
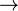
La notation g o f se lit " g rond f ", ou " f suivie de g ". (g o f)(x) se note aussi g o f(x).

Règles

La composition de fonctions n'est valable que si les domaines de définition des fonctions sont compatibles.

Soient et deux fonctions, alors est toujours définie si et seulement si (l'ensemble d'arrivée de la fonction f est compris dans l'ensemble de départ de la fonction g).

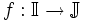
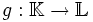
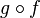
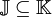
Exemple d'incompatibilité des domaines

Soient les deux fonctions :

et

la fonction est définie uniquement sur le domaine .

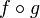
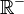
Propriétés

• La composition de fonctions n'est généralement pas commutative :

• La composition de fonctions est associative :

• La composition de fonctions n'est pas distributive (sur un opérateur quelconque ) :

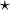
• Continuité : si la fonction g est continue en et la fonction f est continue en alors est continue en .

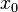
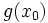
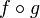
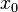
• Composition de deux fonctions f et g strictement monotones :
  • si f et g ont même sens de variation, leur composée est strictement croissante;
  • si f et g ont des sens de variation différents, leur composée est strictement décroissante.

Remarque : Le sens de variation obéit à la régle des signes.

• Dérivée d'une composition de fonctions dérivables :

• • Voir l'article Théorème de dérivation des fonctions composées.

Puissances fonctionnelles

Si Y⊂X alors f peut être composée avec elle-même; et la composée est notée f². Ainsi

Pour tout entier naturel n, la puissance n-ième de f est définie par et .

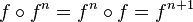
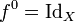
Une extension de cette notation avec des exposants entiers négatifs peut être définie, à condition de supposer la fonction bijective de X sur X. f^-1 désigne l'application réciproque et pour tout entier n strictement négatif fⁿ, est la composée de f^-1 par elle-même -n fois.

Ne pas confondre cette notation avec la puissance d'une fonction pour la multiplication des applications. Par exemple sin² est la fonction sin×sin qui vérifie pour tous réels x, sin²(x) = sin(x)×sin(x). Il y a aussi une confusion possible entre l'inverse d'une fonction pour la multiplication et l'application réciproque.

Autre notation

Au milieu du XX^e siècle, quelques mathématiciens trouvèrent que la notation g o f portait à confusion et décidèrent d'utiliser xf pour f(x) et xfg pour g(f(x)). Ils ne furent pas suivis et cette notation ne se rencontre que dans certains vieux livres.