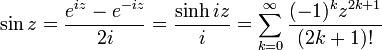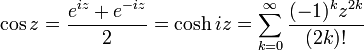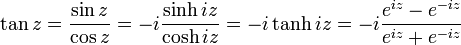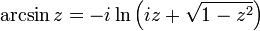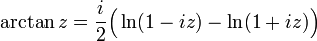Trigonométrie complexe - Définition
Extension des fonctions circulaires
Dans le corps des nombres complexes, grâce aux formules d'Euler, les fonctions trigonométriques peuvent se définir ainsi :
De même que leurs fonctions réciproques :
Ces fonctions souffrent des mêmes problèmes d'indétermination que le logarithme complexe.