Tétraèdre - Définition
  |
|
| Type | Polyèdre régulier |
|---|---|
| Faces | Triangle |
| Éléments : · Faces · Arêtes · Sommets · Caractéristique |
4 6 4 2 |
| Faces par sommet | 3 |
| Sommets par face | 3 |
| Isométries | Td |
| Dual | Tétraèdre |
| Propriétés | Deltaèdre régulier et convexe |
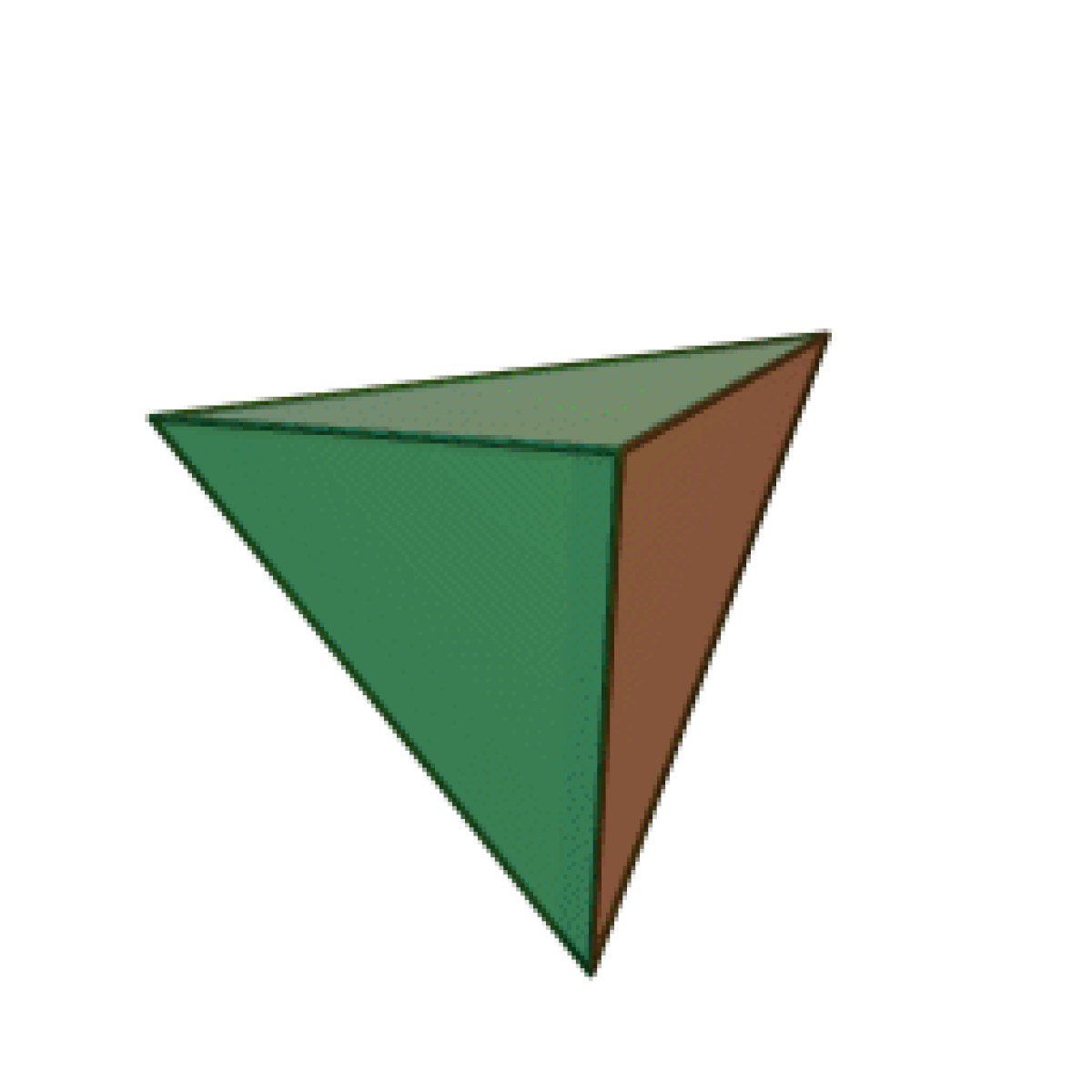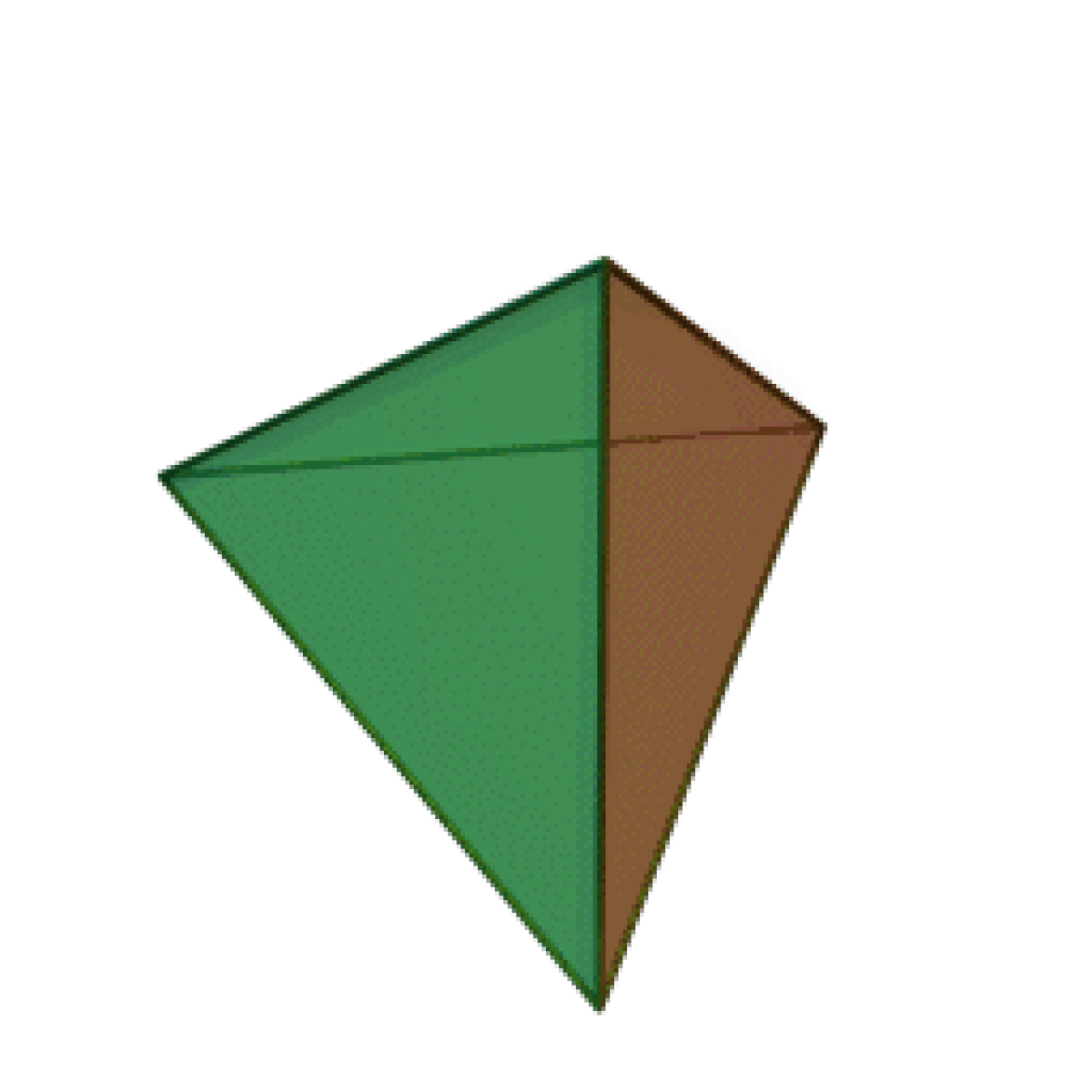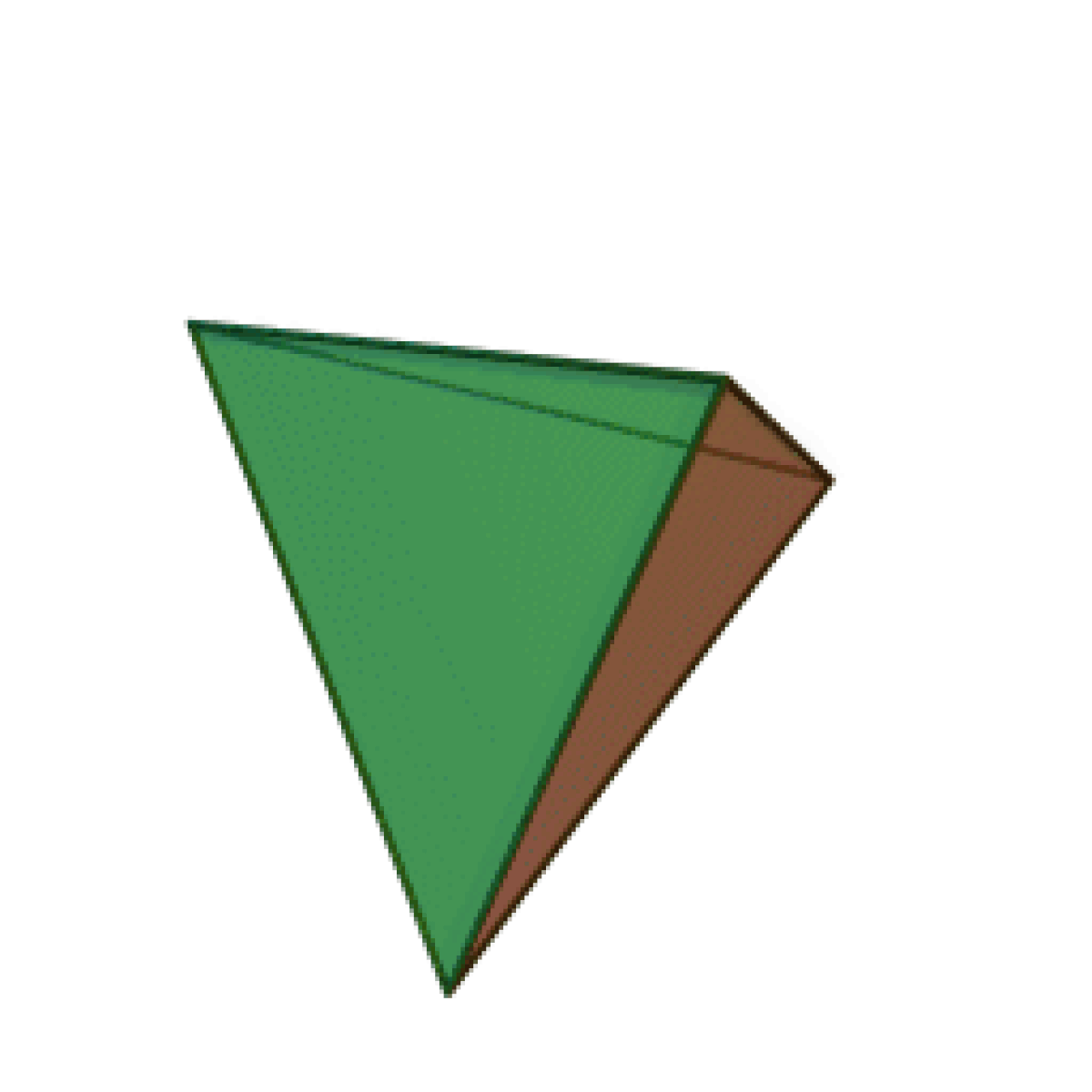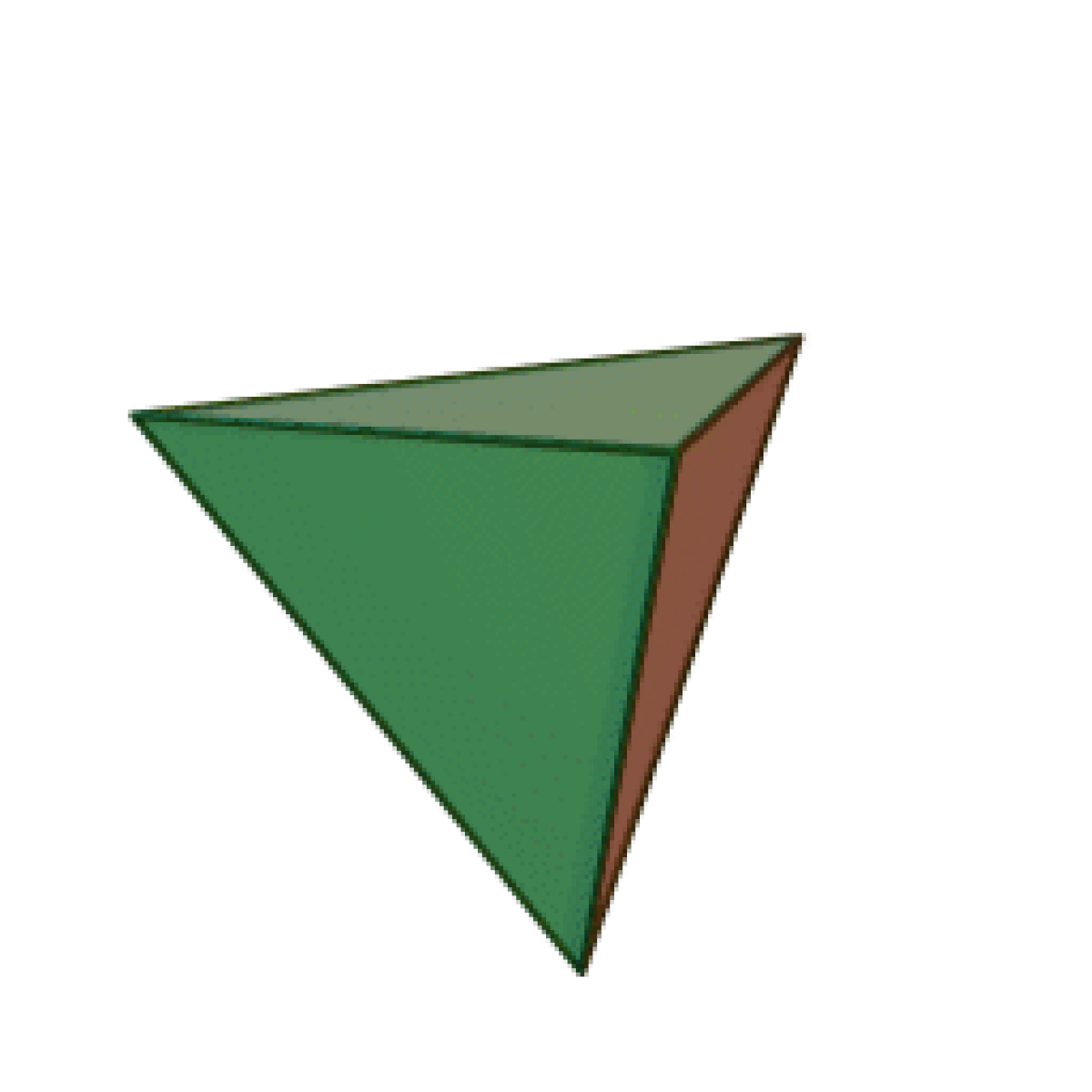
Le tétraèdre (du grec tétra : quatre), est un solide composé de quatre triangles, de la famille des pyramides, donc des cônes.
Le tétraèdre régulier, formé de quatre triangles équilatéraux, fait partie des cinq polyèdres réguliers, ou solides de Platon.
Tétraèdre orthocentrique : un tétraèdre qui a ses 4 hauteurs concourantes est dit orthocentrique. Le point de concours est alors l'orthocentre du tétraèdre.
Le tétraèdre est un simplexe de degré 3.
Le volume d'un tétraèdre est égal à
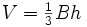
Tétraèdre régulier
Si a est la longueur d'une arête :
- La surface est égale à :
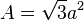
- La hauteur est égale à :
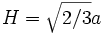
- Le centre du tétraèdre est situé par rapport à la base à :
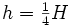
- et le volume à :
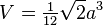
- La valeur du cosinus de l'angle central du tétraèdre régulier est de -1/3 ( c’est-à-dire celui que forment tous les segments qui partent du centre vers les quatre sommets. )
Le tétraèdre est son propre dual, c'est-à-dire qu'en joignant les centres des faces d'un tétraèdre régulier, on obtient un nouveau tétraèdre régulier.
Le groupe des isométries laissant globalement invariant le tétraèdre régulier est isomorphe au groupe symétrique
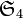
| Les solides géométriques | ||||
| Les solides de Platon | ||||
| Tétraèdre - Cube - Octaèdre - Icosaèdre - Dodécaèdre | ||||
| Les solides d'Archimède | ||||
| Tétraèdre tronqué - Cube tronqué - Octaèdre tronqué - Dodécaèdre tronqué - Icosaèdre tronqué - Cuboctaèdre - Cube adouci - Icosidodécaèdre - Dodécaèdre adouci - Petit rhombicuboctaèdre - Grand rhombicuboctaèdre - Petit rhombicosidodécaèdre - Grand rhombicosidodécaèdre | ||||
| Les solides de Kepler-Poinsot | ||||
| Petit dodécaèdre étoilé - Grand dodécaèdre étoilé - Grand dodécaèdre - Grand icosaèdre | ||||
| Les solides de Catalan | ||||
| Triakioctaèdre - Tétrakihexaèdre - Triakitétraèdre - Pentakidodécaèdre - Triaki-icosaèdre - Dodécaèdre rhombique - Icositétraèdre pentagonal - Triacontaèdre rhombique - Hexacontaèdre pentagonal - Icositétraèdre trapézoïdal - Hexakioctaèdre - Hexacontaèdre trapézoïdal - Hexaki icosaèdre | ||||
| Les solides de Johnson | ||||
| Les solides de révolution | ||||
| Sphère - Cylindre de révolution - Cône de révolution - Tore - Paraboloïde de révolution |