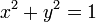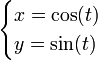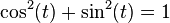Cercle trigonométrique - Définition
Pour la définition de cercle unité vous pouvez consulter le dictionnaire cercle unité.
En mathématiques, le cercle trigonométrique est le cercle de centre l'origine du plan euclidien 
(ou du plan complexe) et de rayon 1.
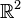
Ce cercle est fréquemment utilisé en trigonométrie, et il est souvent orienté dans le sens direct ou sens trigonométrique, c'est-à-dire dans le sens inverse du sens de rotation des aiguilles d'une montre. Ce sens a été choisi par les astronomes parce qu'il correspond à la rotation de la Terre ; c'est-à-dire le sens dans lequel les étoiles semblent défiler pour un observateur sur Terre.
Soit (x, y) un point de situé dans le premier quadrant et appartenant au cercle trigonométrique. x et y correspondent aux longueurs des côtés adjacents d'un triangle rectangle dont l'hypoténuse est de longueur égale au rayon du cercle, c’est-à-dire 1. Ainsi d'après le théorème de Pythagore, x et y sont liés par la relation
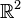
Puisque pour tout x, x2 = ( − x)2, la relation précédente reste valable pour tout point de coordonnées quelconques (c'est-à-dire pas nécessairement situé dans le premier quadrant.)
Réciproquement, tout point (x, y) de tel que
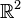
appartient au cercle de centre (0, 0) et de rayon 1 et cette relation s'appelle l'équation cartésienne du cercle trigonométrique.
Fonctions trigonométriques sur le cercle
Notons O=(0, 0). Soit 
un repère orthonormé de 
.
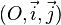
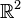
Soit M un point du cercle trigonométrique de coordonnées (x, y), et 
son vecteur associé. Si t, un réel, est une mesure de l'angle 
alors
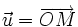
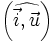
Et l'équation cartésienne du cercle donne immédiatement une identité trigonométrique connue:
Le cercle trigonométrique peut aussi donner un moyen intuitif de réaliser que les fonctions sinus et cosinus sont des fonctions périodiques, vérifiant les relations:
.
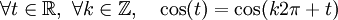
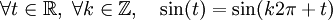
Ces égalités s'interprètent par le fait que le point (x,y) reste le même après que nous ayons ajouté ou retranché un multiple entier de 2π et ainsi effectué plusieurs tours complets du cercle. Lorsqu'elles sont définies à partir d'un triangle rectangle, les valeurs des fonctions sinus, cosinus et d'autres fonctions trigonométriques n'ont de sens que pour des angles compris entre 0 et π/2, mais dans le cercle trigonométrique leurs valeurs prennent un sens en n'importe quel réel.